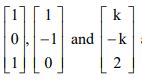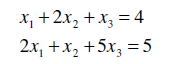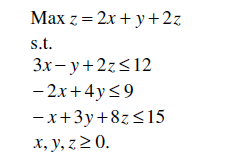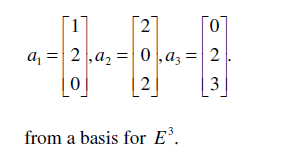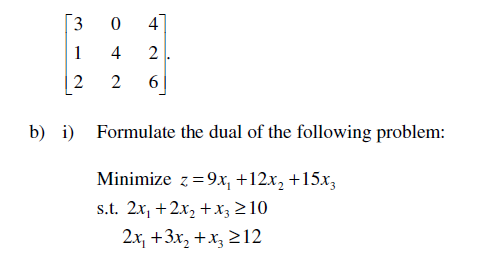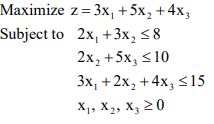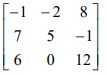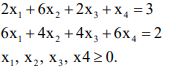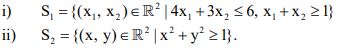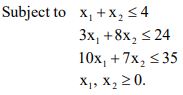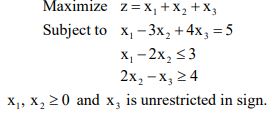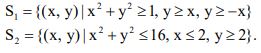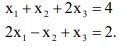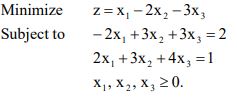IGNOU MTE-12 Linear Programming - Latest Solved Assignment

1. Which of the following statements are true and which are false? Give reasons for your answer.
a) In an LP model, the feasible solution space can be effected when redundant constraints are deleted.
b) If the primal LPP has an optimal solution, then the set of feasible solution to its dual is bounded.
c) In a simplex iteration, an artificial variable can be dropped all together from the simplex table once the variable becomes non basic.
d) The addition of a constant to all the elements of a payoff matrix in a two – person zero sum game can affect only the value of the game, not the optimal mix of the strategies.
e) There may be a balanced transportation problem without any feasible solution.

2. a) A toy company manufactures two types of doll; a basic version-doll A and a deluxe version-doll B. Each doll of type B takes twice as long as to produce as one of type A, and the company would have time to make a maximum 2000 per day if it produce only the basic version. The supply of plastic is sufficient to produce 1500 dolls per day (both A and B combined). The deluxe version requires a fancy dress of which there are only 600 per day available. The company makes profit of ₹3 and 5 per doll respectively on doll A and B. How many of each should be produced per day in order to maximize profit? Solve this problem by graphical method.
b) Find all the basic solutions of the following system:

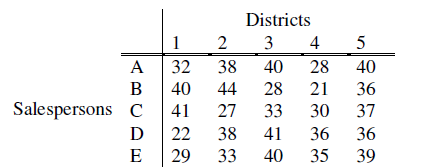
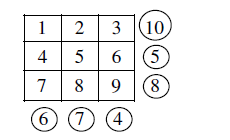
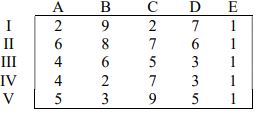
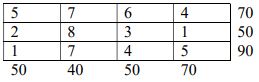
3. a) A marketing manager has 5 salespersons and 5 sales districts. Considering the capabilities of the salespersons and the nature of the districts, the marketing manager estimates the sales per month (in thousand ₹) for each salesperson in each distinct as follows:

Find the assignment of sales persons to districts that will result in maximum sales.
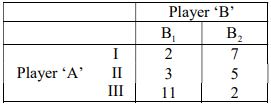
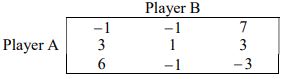
b) Find the maximum and minimax values of the following matrix game.

Does the matrix have a saddle point. Justify your answer.

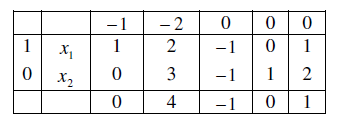
c) The following table is obtained in the intermediate stage while solving an LPP by the simplex method.

Discuss whether an optimal solution will exist or not.

4. a) Solve by simplex method the following linear programming problem:

b) Show that the set of vectors

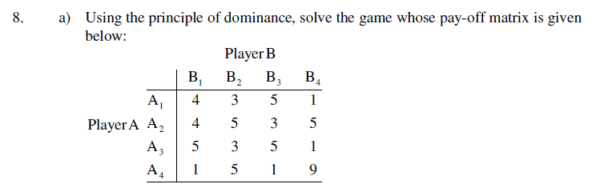
5. a) Use the principle of dominance to reduce the size of the following game. Hence solve the game.

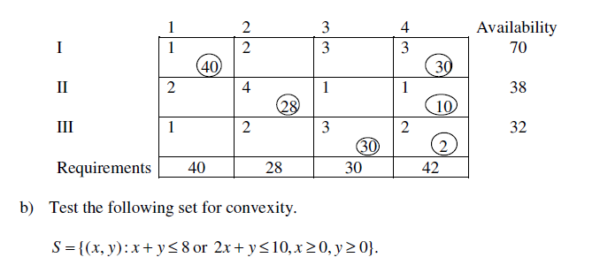
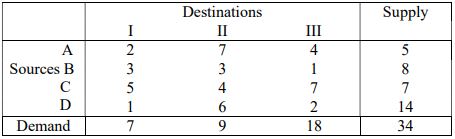
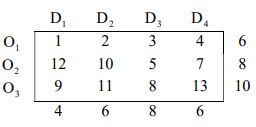
b) Find an initial basic feasible solution for the following transportation problem using matrix-minima method. Also find the transportation cost.

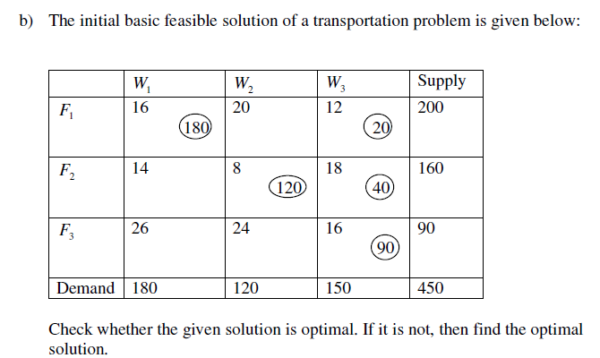
7. a) Using the initial basic feasible solution for the transportation problem given below, find and optimal solution for the problem.

b) Without sketching the region, check whether P(0,0) is in the convex hull of the points A(−1,−1),B(1,0) and C(0,1) . If it is in the region, write P as convex combination of A,B and C.

9. a) A businessman has to get 5 cabinets, 12 desks and 18 shelves cleaned. He has two part-time employees, Anjali and Arnav. Anjali can clean 1 cabinet, 3 desks and 3 shelves in a day, while Arnav can clean 1 cabinet, 2 desks and 3 shelves in a day. Arnav is paid ₹22 per day and Anjali is paid ₹ 25 per day. Formulate the problem of finding the number of days for which Anjali and Arnav have to be employed to get the cleaning done with minimum cost as a linear programming problem.
b) For the following pay-off matrix, transform the zero-sum game into an equivalent linear programming problem: 

1. Which of the following statements are true and which are false? Give a short proof or a counter-example in support of your answer.

a) In a two-dimensional LPP solution, the objective function can assume the same value at two distinct extreme points.
b) Both the primal and dual of an LPP can be infeasible.
c) An unrestricted primal variable converts into an equality dual constraint.
d) In a two-person zero-sum game, if the optimal solution requires one player to use a pure strategy, the other player must do the same.
e) If 10 is added to each entry of a row in the cost matrix of an assignment problem, then the total cost of an optimal assignment for the changed cost matrix will also increase by 10.

2. a) Solve the following linear programming problem using simple method:

b) Using the principle of dominance, reduce the size of the following game:

Hence solve the game.

3. a) Find all basic feasible solutions for the following set of equations:

b) Examine convexity of the following sets:

4. a) Solve the following linear programming problem by graphical method:

b) Find the dual of the following LPP:

5. a) Find the initial basic feasible solution of the following transportation problem using matrix-minima method:

Also, find the optimal solution.

b) Solve the following game graphically:

6. a) A firm manufactures two types of products, A and B, and sells them at a profit of ₹2 on type A and ₹ 3 on type B. Each product is processed on two machines M1 and M2. Type a requires one minute of processing time on M1 and two minutes on M2; type B requires one minute on M1 and one minute on M2. The machine M1 is available for not more than 6 hours 40 minutes while machine M2 is available for 10 hours during any working day.
Formulate the problem at LPP.

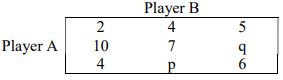
b) Solve the following assignment problem:

7. a) The following table is obtained in the intermediate state while solving an LPP by simplex method:

Check whether an optimal solution of the LPP will exist or not.

b) Write the LPP model of the following transportation problem:

c) Find the range of values of p and q which will render the entry (2, 2), a saddle point for the following game:

8. a) Test the convexity of the following sets:

b) Determine all the basic feasible solutions to the equations

Identify the degenerate basic feasible solutions.

9. a) Let 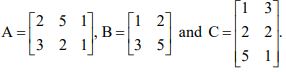 Compute AB, BC, AC, if they exists, otherwise, give reason for their non-existence.
b) Solve the following LPP:

c) Find the saddle point (if exists) in the following pay-off matrix:

Also, find the value of the game.

10. a) Determine an initial basic feasible solution to the following transportation problem and hence find an optimal solution to the problem:

b) Find all values of k for which the vectors  are linearly independent.