IGNOU MTE-13 Discrete Mathematics - Latest Solved Assignment

1. Check whether the following statements are true or not. Justify your answers with a short proof or a counter example.

i) If the contrapositive of a statement is true, then the statement itself is also true.
ii) an +3an-1 + 2an-2 = 2n is a linear homogeneous recurrence relation.
iii) A particular solution of the recurrence relationan an – 2an-1 + an-2 =1 has the form C n2.
iv) The edge chromatic number of the graph 𝐾6 is 5.
v) If a dice is rolled thrice, then the probability of getting a 6 each time is 1/72.
vi) Every odd cycle has the same chromatic and edge chromatic numbers.
vii) Every Eulerian graph is Hamiltonian.
viii) gives the number of ways in which any 3 objects can be placed in any 4 boxes.
ix) There exists a self-complementary planar graph on 5 or more vertices.
x) The number of partitions of 6 is 10.

2. a) Draw the logic circuit for the Boolean expression ((x1 ∧ x2)′ ∨ x3)′ ∧ x2.
b) Express the following statements in symbolic form.
i) There is a man in the park with blue eyes.
ii) Every blue-eyed man in the park is wearing a red hat.
iii) If a man wears no hat, then he has black eyes.
c) Using generating functions find Sn = 1+ 2 + 3 + …. + n.

3. a) There are about 77 crore ways to arrange the letters of the word “COMBINATORICS”. Count the exact number of such ways.
b) Solve the recurrence relation:
an – 6an-1 + 9an-2 = 3n
c) List all the onto mappings from the set {a,b,c,d} to {1,2,3,4}. How many onto mappings are there form {a,b,c,d} to {1,2,3,4,5}?
d) For any statements p, q and r, prove that ( p → q) ∧ (~ q → r) ∧ r ∧ ~ q ⇒~ p.

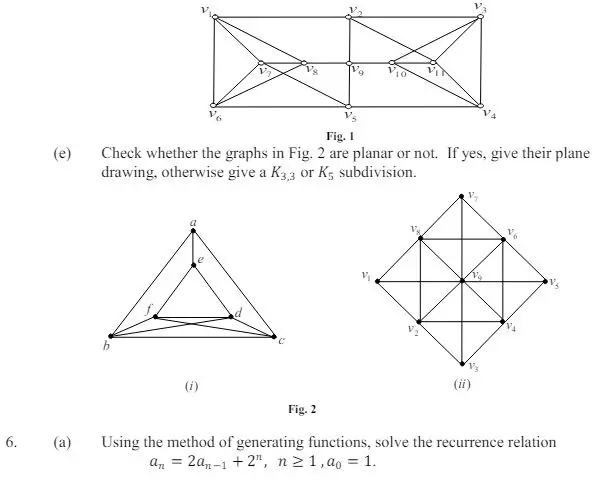
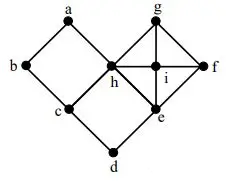
4. a) Draw three nonisomorphic induced subgraphs of the following graph, each having the same number of vertices. Justify your choice.

b) Is the complement of the Peterson graph planar? Justify your answer.
c) What do you understand by a subdivision of a graph? Is every subdivision of a Hamiltonian graph Hamiltonian? Justify.

5. a) Let 𝐶𝑛 denote the number of 𝑛-tuples whose entries are 0 or 1 only, and two consecutive entries of which are zero.
i) Find 𝐶1 and 𝐶2.
ii) Find a recurrence relation for 𝐶𝑛.

b) write down and count all the partitions of the number 7. To verify your answer use the generating function for Pn, taking n = 7 in Theorem 5 (of Unit 5, Block2).

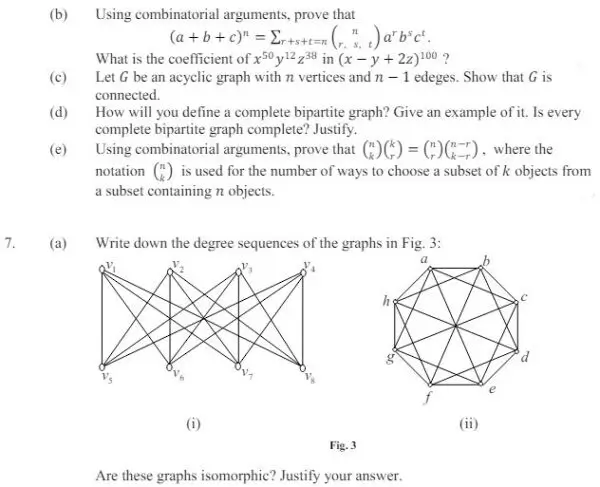
6. a) Express x5 in terms of falling factorials and hence evaluate  for m = 0,1,2,3,4,5.
b) Find a recurrence relation for an , the number of ways to arrange cars in a row with n spaces if we can use Maruti 800, Tata Safari or Scorpio. A Tata Safari or Scorpio requires two spaces, whereas a Maruti 800 requires just one space. Assume that you have unlimited number of each type of car and we do not distinguish between 2 cars of the same type.
c) Define the nth Bell number. Using the formula for Bell numbers or otherwise, determine 𝐵5 .
d) Show that if 7 colours are used to paint 50 bicycles and each bicycle is coloured with a single colour, at least 8 bicycles will have the same colour.

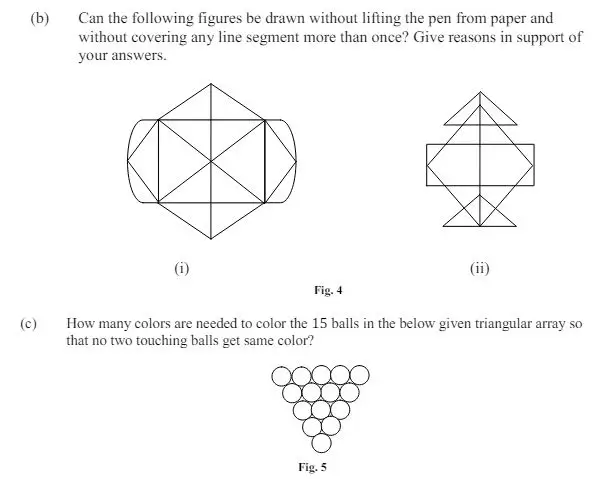
7. a) Let T be a graph such that between every two vertices of it there is exactly one path. Show that T is a tree.
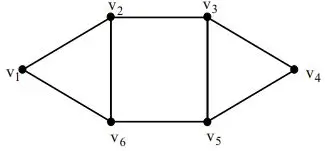
b) Define vertex connectivity and cut vertex set of any graph G. Find the vertex connectivity and cut vertex set for the following graph:

c) How many numbers from 0 to 759 are not divisible by either 3 or 7?

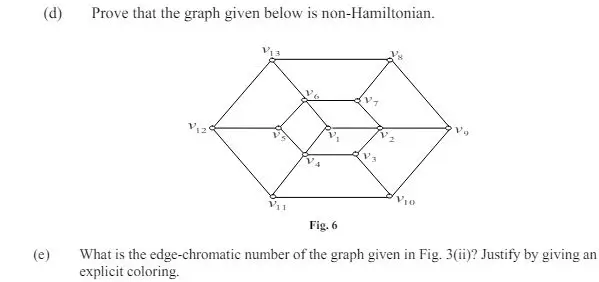
8. a) Solve the recurrence relation:
an = 2an-1 + 1 if n ≥ 1 and a0 = 0,
using generating function technique. Also find a5 using your answer.
b) Is there a 4-regular graph on 7 vertices? Justify your answer.
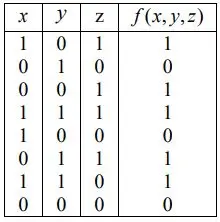
c) Find the Boolean expression in the DNF form for the function defined in tabular form below: