Help?
PLEASE MATCH YOUR ASSIGNMENT QUESTIONS ACCORDING TO YOUR SESSION
IGNOU MST-11 (June 2024 – June 2025) Assignment Questions
1. Solve the following problems.
(a) A ball is thrown in an upward direction. If the variable x represents the velocity of the ball when it strikes the ground. Classify variable x as discrete or continuous. Justify your answer with a proper explanation.
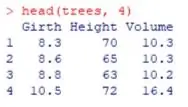
(b) In R we have a built-in data set “trees”. A screenshot of the first four rows together with the R code to obtain it is given as follows. To get more detail about this data set you can run ?trees command on R console.
Note that all the three variables of this data set are numeric. So, assuming each row of this data set is a point in 3-dimension. Find the distances between the points corresponding to the first and the third rows using the Manhattan and Chebyshev distance formula.
(c) Find the equation of a line passing through points A(2, 3, 5) and B(5, 8, 9). Also, find the coordinates of a point on this line which is at a distance of 10 units from point A opposite to the side of point B.
(d) Give an example of a set which is convex but not affine. Justify your claim with a proper explanation.
2. (a) Test the convergence of the series 
(b) If 
be a function defined by f(x)= x2+2x+1, x ∈ [0, 5]. Show that f is Riemann integrable using both definitions. Also, verify that the results of both definition match.
3. (a) Evaluate the integral 
by considering D as a region of Type I and then as a region of Type II.
(b) Evaluate the integral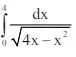 
using beta and gamma functions.
IGNOU MST-11 (January 2024 – December 2024) Assignment Questions
1. Solve the following problems.
(a) A ball is thrown in an upward direction. If the variable x represents the velocity of the ball when it strikes the ground. Classify variable x as discrete or continuous. Justify your answer with a proper explanation.
(b) In R we have a built-in data set “trees”. A screenshot of the first four rows together with the R code to obtain it is given as follows. To get more detail about this data set you can run ?trees command on R console.
Note that all the three variables of this data set are numeric. So, assuming each row of this data set is a point in 3-dimension. Find the distances between the points corresponding to the first and the third rows using the Manhattan and Chebyshev distance formula.
(c) Find the equation of a line passing through points A(2, 3, 5) and B(5, 8, 9). Also, find the coordinates of a point on this line which is at a distance of 10 units from point A opposite to the side of point B.
(d) Give an example of a set which is convex but not affine. Justify your claim with a proper explanation.
2. (a) Test the convergence of the series
(b) If be a function defined by f(x)= x2+2x+1, x ∈ [0, 5]. Show that f is Riemann integrable using both definitions. Also, verify that the results of both definition match.
3. (a) Evaluate the integral by considering D as a region of Type I and then as a region of Type II.
(b) Evaluate the integral using beta and gamma functions.
