Help?
PLEASE MATCH YOUR ASSIGNMENT QUESTIONS ACCORDING TO YOUR SESSION
IGNOU MST-12 (June 2024 – June 2025) Assignment Questions
1. (a) Suppose two friends Anjali and Prabhat trying to meet for a date to have lunch say between 2 pm to 3 pm. Suppose they follow the following rules for this meeting:
• Each of them will reach either on time or 10 minutes late or 20 minutes late or 30 minutes late or 40 minutes late or 50 minutes late or 1 hour late. All these arrival times are equally likely for both of them.
• Whoever of them reaches first will wait for the other to meet only for 10 minutes. If within 10 minutes the other does not reach, he/she leaves the place and they will not meet.
Find the probability of their meeting.
(b) In the study learning material (SLM), you have seen many situations where Poisson distribution is suitable and discussed some examples of such situations. Create your own example for a situation other than those that are discussed in SLM. If you denote your created random variable by X then find the probability that X is less than 2.
2. (a) In an election there are two candidates. Being a statistician, you are interested in predicting the result of the election. So, you plan to conduct a survey. Using the learning skill of this course answer the following question. How many people should be surveyed to be at least 90% sure that the estimate is within 0.03 of the true value?
(b) Let 
be a probability space and X1,X2,X3,…. be a sequence of independent and identically distributed (i.i.d.) random variables from the uniform distribution on the interval [12, 20]. If 
denotes the sample mean of the first n random variables of the sequence X1,X2,X3,…., and 
Find the value of a.
3. Explain the procedure of assigning probability in a continuous world of probability theory
4. (a) If X ~ Gamma , and Y ~ Gamma , (θ α) (θ β) be two independent gamma distributions and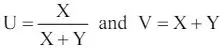 
then find the distribution of U.
(b) A hospital specialising in heart surgery. In 2022 total of 2000 patients were admitted for treatment. The average payment made by a patient was Rs 1, 50,000 with a standard deviation of Rs 25000. Under the assumption that payments follow a normal distribution, answer the following questions.
(i) The number of patients who paid between Rs 1,40,000 and Rs 1,70,000.
(ii) The probability that a patient bill exceeds Rs 1,00,000.
(iii) Maximum amount paid by the lowest paying one-third of patients.
IGNOU MST-12 (January 2024 – December 2024) Assignment Questions
1. (a) Suppose two friends Anjali and Prabhat trying to meet for a date to have lunch say between 2 pm to 3 pm. Suppose they follow the following rules for this meeting:
• Each of them will reach either on time or 10 minutes late or 20 minutes late or 30 minutes late or 40 minutes late or 50 minutes late or 1 hour late. All these arrival times are equally likely for both of them.
• Whoever of them reaches first will wait for the other to meet only for 10 minutes. If within 10 minutes the other does not reach, he/she leaves the place and they will not meet.
Find the probability of their meeting.
(b) In the study learning material (SLM), you have seen many situations where Poisson distribution is suitable and discussed some examples of such situations. Create your own example for a situation other than those that are discussed in SLM. If you denote your created random variable by X then find the probability that X is less than 2.
2. (a) In an election there are two candidates. Being a statistician, you are interested in predicting the result of the election. So, you plan to conduct a survey. Using the learning skill of this course answer the following question. How many people should be surveyed to be at least 90% sure that the estimate is within 0.03 of the true value?
(b) Let be a probability space and X1,X2,X3,…. be a sequence of independent and identically distributed (i.i.d.) random variables from the uniform distribution on the interval [12, 20]. If denotes the sample mean of the first n random variables of the sequence X1,X2,X3,…., and Find the value of a.
3. Explain the procedure of assigning probability in a continuous world of probability theory
4. (a) If X ~ Gamma , and Y ~ Gamma , (θ α) (θ β) be two independent gamma distributions and 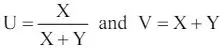then find the distribution of U.
(b) A hospital specialising in heart surgery. In 2022 total of 2000 patients were admitted for treatment. The average payment made by a patient was Rs 1, 50,000 with a standard deviation of Rs 25000. Under the assumption that payments follow a normal distribution, answer the following questions.
(i) The number of patients who paid between Rs 1,40,000 and Rs 1,70,000.
(ii) The probability that a patient bill exceeds Rs 1,00,000.
(iii) Maximum amount paid by the lowest paying one-third of patients.
