Bought By: 13692
Rating: 4.9

Get Good Marks in your B.Sc. Mathematics Programme in the Term-End Exams even if you are busy in your job or profession.
We've sold over 64,128,639 Help Books and Delivered 80,914,783 Assignments Since 2002.
As our customers will tell you...yes, it really result-oriented.









 2. a) In the past, the standard deviation of weights of 100 gm packages of tea leaves filled by a machine was 0.8 gm. A sample of 20 packages was drawn and its s.d. was found to be 1.0 gm. Assuming normality at 5% level of significance, test the hypothesis that the population s.d. σ = 8.0 against the alternative hypothesis that s.d. σ > 08.0 .
b) Find the correlation coefficient for data with 20 pairs of values of x and y, if it is given that
2. a) In the past, the standard deviation of weights of 100 gm packages of tea leaves filled by a machine was 0.8 gm. A sample of 20 packages was drawn and its s.d. was found to be 1.0 gm. Assuming normality at 5% level of significance, test the hypothesis that the population s.d. σ = 8.0 against the alternative hypothesis that s.d. σ > 08.0 .
b) Find the correlation coefficient for data with 20 pairs of values of x and y, if it is given that
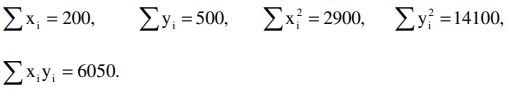 c) Explain the following terms of quality control with suitable examples:
i) Process Capability
ii) Tolerance
3. a) i) Write the sample space of the experiment of drawing 3 screws from a box of right-handed (R) and left-handed (L) screws.
ii) If event A: At least one R is drawn
event B: At least one L is drawn
event C: Exactly 2 right-handed screws are drawn
event D: Exactly 2 left-handed screws are drawn
Are the events A and B mutually exclusive? Are C and D mutually exclusive? Justify your answer.
b) The sick leave time for workers in a factory is normal with mean 1000 hours and s.d. 100 hours, per month. How much time t should be budgeted next month exceeds the time corresponding to the probability 20%.
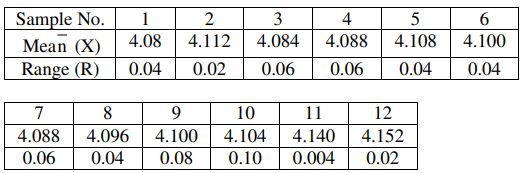
c) Find the moving averages of length 3 for the following data. Also, plot these averages.
c) Explain the following terms of quality control with suitable examples:
i) Process Capability
ii) Tolerance
3. a) i) Write the sample space of the experiment of drawing 3 screws from a box of right-handed (R) and left-handed (L) screws.
ii) If event A: At least one R is drawn
event B: At least one L is drawn
event C: Exactly 2 right-handed screws are drawn
event D: Exactly 2 left-handed screws are drawn
Are the events A and B mutually exclusive? Are C and D mutually exclusive? Justify your answer.
b) The sick leave time for workers in a factory is normal with mean 1000 hours and s.d. 100 hours, per month. How much time t should be budgeted next month exceeds the time corresponding to the probability 20%.
c) Find the moving averages of length 3 for the following data. Also, plot these averages.
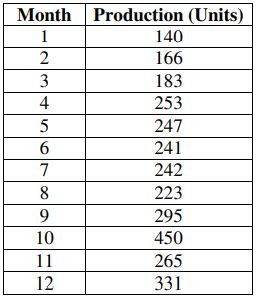 4. a) Find the mean and variance of the following data:
4. a) Find the mean and variance of the following data:
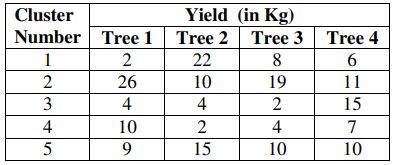 Estimate the average yield (in kg) per tree of guava using cluster sampling method and simple random sampling method.
5. a) A sample of 6 boxes is to be selected from 30 boxes of mangoes numbered 1 to 30. Find the samples using:
i) Direct WR method
ii) Remainder approach
iii) Quotient approach, stating clearly the starting random numbers chosen by you.
b) Find the regression line of y on x
Estimate the average yield (in kg) per tree of guava using cluster sampling method and simple random sampling method.
5. a) A sample of 6 boxes is to be selected from 30 boxes of mangoes numbered 1 to 30. Find the samples using:
i) Direct WR method
ii) Remainder approach
iii) Quotient approach, stating clearly the starting random numbers chosen by you.
b) Find the regression line of y on x
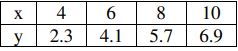 6. a) A random sample of size 4 is taken from each of 3 independent normal random variables X1, X2, X3 resulting in the following data:
6. a) A random sample of size 4 is taken from each of 3 independent normal random variables X1, X2, X3 resulting in the following data:
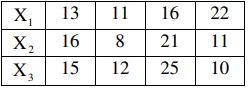 Assuming that the 3 variables have equal variances, test at the 0.05 significance level, the hypothesis that X1, X2, X3 have the same mean using ANOVA. You may like to use following values.
b) Suppose you are waiting at a bus stand for a bus. Every 10 minutes, you are recording the number of buses that pass by you. Data recorded is as follows:
Assuming that the 3 variables have equal variances, test at the 0.05 significance level, the hypothesis that X1, X2, X3 have the same mean using ANOVA. You may like to use following values.
b) Suppose you are waiting at a bus stand for a bus. Every 10 minutes, you are recording the number of buses that pass by you. Data recorded is as follows:
 Identify the distribution, the buses follow. Calculate the average number of buses that pass you and the variance.
7. a) In the amount of cosmic radiations to which a person is exposed while flying across a specific continent is a normal random variable with mean 4.35 units and S.D. 0.59 units. Find the probabilities that the amount of exposure during such a flight is (i) between 4.00 and 5.00 units, (ii) at least 5.50 units.
b) A sampling random sample of size 100 has mean 15 and population variance 25. Find an interval estimate of the population mean with a confidence level of 99% and 95%.
c) A hypothetical population consists of the numbers 2, 5 and 7. Write all possible simple random samples of size 2 (with replacement). Verify that the sample mean is an unbiased estimator of the population mean.
8. a) The following random samples are measurements of the heat producing capacity in millions of calories per ton of specimens of coal from mines:
Identify the distribution, the buses follow. Calculate the average number of buses that pass you and the variance.
7. a) In the amount of cosmic radiations to which a person is exposed while flying across a specific continent is a normal random variable with mean 4.35 units and S.D. 0.59 units. Find the probabilities that the amount of exposure during such a flight is (i) between 4.00 and 5.00 units, (ii) at least 5.50 units.
b) A sampling random sample of size 100 has mean 15 and population variance 25. Find an interval estimate of the population mean with a confidence level of 99% and 95%.
c) A hypothetical population consists of the numbers 2, 5 and 7. Write all possible simple random samples of size 2 (with replacement). Verify that the sample mean is an unbiased estimator of the population mean.
8. a) The following random samples are measurements of the heat producing capacity in millions of calories per ton of specimens of coal from mines:
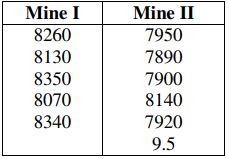 Test at 5% level of significance whether the difference between the means of two samples is significant?
b) A company operates four machines on three separate shifts daily. The following table presents the data for machine break-downs resulted during a 6 month time period:
Test at 5% level of significance whether the difference between the means of two samples is significant?
b) A company operates four machines on three separate shifts daily. The following table presents the data for machine break-downs resulted during a 6 month time period:
 At 5% level of significance test the hypothesis that for an arbitrary breakdown in the machine causing the breakdown and the shifts are independent.
9. a) The three drying techniques for curing a glue were studied and the following times were observed:
At 5% level of significance test the hypothesis that for an arbitrary breakdown in the machine causing the breakdown and the shifts are independent.
9. a) The three drying techniques for curing a glue were studied and the following times were observed:
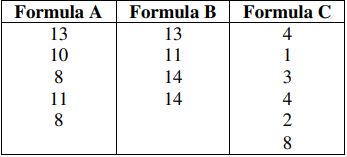 At α = 0.05, test the hypothesis that the average times for three formulae are same
b) The following data represent the number of defects discovered at a factory on 20 successive batches of 10 cars each:
At α = 0.05, test the hypothesis that the average times for three formulae are same
b) The following data represent the number of defects discovered at a factory on 20 successive batches of 10 cars each:
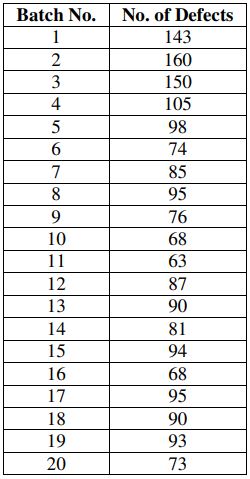 Does it appear that the production process is in statistical control throughout? Give justification.
10. Which of the following statements are true and which are false?
a) If X is continuous random variables following uniform distribution with values in [2, 6] then P (X = 4) = 0
b) A 90% confidence interval calculated using a sample of size 40 is smaller than the one calculated using a sample of size 100.
c) If a dice is rolled twice, then the number of possible outcomes is 36.
d) If every 5th student on the roll is selected and her height is measured, the sampling method used is simple random sampling.
e) A type I error is committed when we fail to reject a null hypothesis when the alternative hypothesis is true.
Does it appear that the production process is in statistical control throughout? Give justification.
10. Which of the following statements are true and which are false?
a) If X is continuous random variables following uniform distribution with values in [2, 6] then P (X = 4) = 0
b) A 90% confidence interval calculated using a sample of size 40 is smaller than the one calculated using a sample of size 100.
c) If a dice is rolled twice, then the number of possible outcomes is 36.
d) If every 5th student on the roll is selected and her height is measured, the sampling method used is simple random sampling.
e) A type I error is committed when we fail to reject a null hypothesis when the alternative hypothesis is true.To attend IGNOU AST-01 Term-End Examination, you must first submit your Assignments to the university and it is possible from the AST-01 study material. You can solve all necessary Assignments using Help Books. This will help in gaining good marks.
All best wishes with our efforts that you do not meet any obstacle before attending examinations next year. You can pass the B.Sc. Mathematics Programme Annual Exams with a good grade using Books/Materials from any one place at home or anywhere else!
ALL THE BEST!!!
Team GullyBaba