PART A
1. a) Write the assumptions of kinetic theory of gases. Derive the following expression of the pressure exerted by an ideal gas:
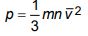
Also, using this expression deduce Avogadro’s law. What is the kinetic interpretation temperature?
b) The expression for the number of molecules in a Maxwellian gas having speeds in the range v to v + dv is given by
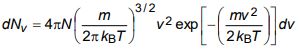
Obtain an expression of average speed and root mean square speed of a molecule.
c) Define mean free path of the molecules of a gas. Show that it is equal to
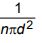
under Zeroth order approximation.
d) What is Brownian motion? Write any four characteristics of Brownian motion.
2. a) What are Intensive and extensive variables. Write two examples of each. List the intensive and extensive variables required to specify the thermodynamic systems
(i) paramagnetic solid and (ii) stretched wire.
b) State Zeroth law of thermodynamics. Discuss how this law introduces the concept of temperature. Write parametric as well as exact equation of state for one mole of a real gas and paramagnetic substance.
c) For a pVT – system, show that:
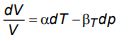
where βT is the isothermal compressibility and α is isobaric coefficient of volume expansion.
d) What is an adiabatic index? Using the first law of thermodynamics, show that, TV-1 = K when one mole of an ideal gas is made to undergo quasi-static adiabatic expansion.
e) Derive an expression for the work done in an isothermal process of an ideal gas.
PART B
3. a) Define efficiency of a Carnot engine. A Carnot engine has an efficiency of 50% when its sink temperature is at 27°C. Calculate the source temperature for increasing its efficiency to 60%.
b) State third law of thermodynamics. Write its mathematical expression. Discuss some important consequences of third law.
c) Write Maxwell’s relations and using these relations derive first and second energy equations.
d) Derive Clausius-Clapeyron equation for two phases to coexist in equilibrium.
e) What is Joule-Thomson effect? Write the mathematical expression of Joule Thomson Coefficient for van der Waals’ gas. What will be the effect on gas if the intermolecular forces are strong?
4. a) Obtain an expression of single particle partition function. Hence, using this expression obtain expressions for entropy and pressure.
b) Define phase space of the system. Draw the phase space for a linear harmonic oscillator.
c) Establish the Boltzmann relation S = kB lnW.
d) Show that Bose derivation of Planck’s law for energy density is given by
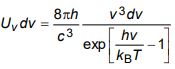
PART A
1. a) Calculate the temperature at which root mean square speed of nitrogen molecules exceeds their most probable speed by 200 ms-1. Take mN2 = 28 kg kmol -1 .
b) Using the relation
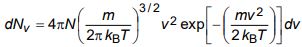
for the number of molecules in a Maxwellian gas having speeds in the range v to v + dv, obtain an expression for (i) average speed, and (ii) root mean square speed.
c) Derive the survival equation for distribution of free paths. Hence, plot distribution of free paths as a function of x/λ.
d) Calculate the diffusion coefficient of hydrogen molecules at 27°C when pressure is 3 atm. Assume that it behaves as a Maxwellian gas. Take rH2 = 1.37 x 10-10 m and kB = 1.38 x 10 -23 JK .
e) Define Brownian motion. Write its four observed characteristics.
2. a) What do you understand by (i) isobaric (ii) isochoric (iii) isothermal, and (iv) cyclic processes? Represent these processes on p-V diagrams.
b) Prove that for a pVT-system
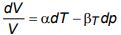
where α is the isobaric coefficient of volume expansion and βT is isothermal compressibility.
c) Write the differential form of first law of thermodynamics. Show that for an ideal gas, it can be written as δQ = CVdT + pdV. Using this result for one mole of an ideal gas which undergo quasi-static adiabatic expansion, obtain the expression , TV γ -1= K where γ is the ratio of heat capacity at constant pressure to that at constant volume.
d) Two moles of an ideal gas at STP is expanded isothermally to thrice its volume. It is then made to undergoes isochoric change to attain its original pressure. Calculate the total work done in these processes. Take R = 8.3 JK-1 mol-1.
PART B
3. a) Write Kelvin-Planck and Clausius statements of the second law of thermodynamics. Show that these two statements are equivalent.
b) Calculate the change in entropy when 20 g of ice at 0°C is converted into steam.
[Given: latent heat of fusion of ice = 80 cal g-1, latent heat of fusion of steam = 540 cal g-1].
c) Using Maxwell’s relations, deduce first and second TdS-equations. Also, obtain the first TdS-equation in terms of volume expansivity (α) and isothermal compressibility (βT).
d) State Stefan-Boltzmann’s law of black body radiation. Plot spectral energy density of a black body with wavelength at different temperatures and discuss the results of these plots.
4. a) Derive Boltzmann entropy relation S = kB ln W, where W is a thermodynamic probability.
b) Using the expression of thermodynamic probability of a Fermi-Dirac system, derive the expression for the distribution function and plot it as a function of energy at temperatures (i) T = 0 K and (ii) T > 0 K.
c) A box of volume 1cm3 contains 4 x 10 21 electrons. Calculate Fermi energy of these electrons. [Take: me = 9.1 x 10-28 g and h = 6.62 x 10-28 erg s].
d) Write the expression for N distinguishable particles partition function for an ideal gas and hence obtain expressions for heat capacity at constant (i) volume, and (ii) pressure.

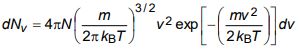 Obtain an expression of average speed and root mean square speed of a molecule.
c) Define mean free path of the molecules of a gas. Show that it is equal to
Obtain an expression of average speed and root mean square speed of a molecule.
c) Define mean free path of the molecules of a gas. Show that it is equal to 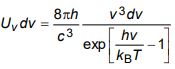
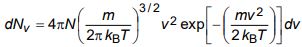 for the number of molecules in a Maxwellian gas having speeds in the range v to v + dv, obtain an expression for (i) average speed, and (ii) root mean square speed.
c) Derive the survival equation for distribution of free paths. Hence, plot distribution of free paths as a function of x/λ.
d) Calculate the diffusion coefficient of hydrogen molecules at 27°C when pressure is 3 atm. Assume that it behaves as a Maxwellian gas. Take rH2 = 1.37 x 10-10 m and kB = 1.38 x 10 -23 JK .
e) Define Brownian motion. Write its four observed characteristics.
2. a) What do you understand by (i) isobaric (ii) isochoric (iii) isothermal, and (iv) cyclic processes? Represent these processes on p-V diagrams.
b) Prove that for a pVT-system
for the number of molecules in a Maxwellian gas having speeds in the range v to v + dv, obtain an expression for (i) average speed, and (ii) root mean square speed.
c) Derive the survival equation for distribution of free paths. Hence, plot distribution of free paths as a function of x/λ.
d) Calculate the diffusion coefficient of hydrogen molecules at 27°C when pressure is 3 atm. Assume that it behaves as a Maxwellian gas. Take rH2 = 1.37 x 10-10 m and kB = 1.38 x 10 -23 JK .
e) Define Brownian motion. Write its four observed characteristics.
2. a) What do you understand by (i) isobaric (ii) isochoric (iii) isothermal, and (iv) cyclic processes? Represent these processes on p-V diagrams.
b) Prove that for a pVT-system