Bought By: 30023
Rating: 4.5
Get Good Marks in your B.Sc. Physics Programme in the Term-End Exams even if you are busy in your job or profession.
We've sold over 64,249,982 Help Books and Delivered 81,076,370 Assignments Since 2002.
As our customers will tell you...yes, it really result-oriented.
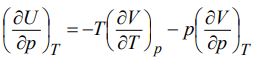 Discuss its physical significance
4. a) State the principle of equipartition of energy. Write a relation between number of degrees of freedom, number of particles constituting the system and the total number of constraints. Calculate the degrees of freedom for (i) single atom, (ii) diatomic molecule.
b) Derive Einstein’s formula for mean square displacement of a Brownian particle.
c) Calculate the coefficient of viscosity of hydrogen at STP. Take
ρ = 8.90 × 10–2 kg m–3, λ = 2 × 10–7 m and kB = 1.38 × 10 –23 JK–1.
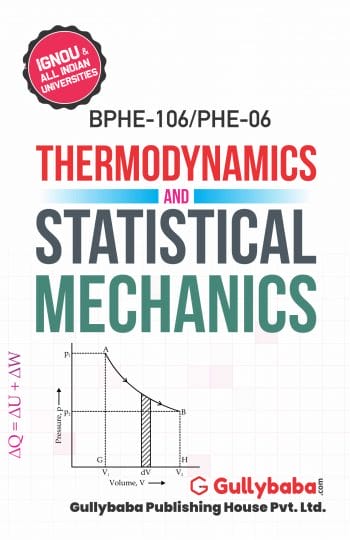
5. a) Establish Boltzmann relation between entropy (S), and thermodynamic probability (W):
S = kB ln W.
b) What is a Gibbs paradox? How did it arise?
c) Using the expression of Bose-Einstein distribution function for photons
Discuss its physical significance
4. a) State the principle of equipartition of energy. Write a relation between number of degrees of freedom, number of particles constituting the system and the total number of constraints. Calculate the degrees of freedom for (i) single atom, (ii) diatomic molecule.
b) Derive Einstein’s formula for mean square displacement of a Brownian particle.
c) Calculate the coefficient of viscosity of hydrogen at STP. Take
ρ = 8.90 × 10–2 kg m–3, λ = 2 × 10–7 m and kB = 1.38 × 10 –23 JK–1.
5. a) Establish Boltzmann relation between entropy (S), and thermodynamic probability (W):
S = kB ln W.
b) What is a Gibbs paradox? How did it arise?
c) Using the expression of Bose-Einstein distribution function for photons
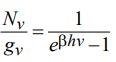 derive Plancks Law and show that (i) Rayleigh-Jeans Law, and (ii) Wien’s Law follow from it at low & high frequencies.
derive Plancks Law and show that (i) Rayleigh-Jeans Law, and (ii) Wien’s Law follow from it at low & high frequencies.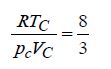 d) Derive an expression for survival equation for distribution of free paths. Also, plot survival equation.
e) Derive Einstein formula for mean square displacement of a Brownian particle.
2. a) Describe the construction and working of a Platinum resistance thermometer. Write its two principal merits.
b) Define the followings with example: (i) Intensive variables (ii) Extensive variables (iii) Adiabatic boundary (iv) Open system (v) Isolated system.
c) Obtain the expression for isothermal compressibility (βT) and coefficient of volume expansion (α) for a van der Waals’ gas.
d) Obtain an expression for work done by an ideal gas in an adiabatic process. Two litre of an ideal gas at a pressure of 5 atm expands adiabatically to two times its initial volume. Calculate the work done by the gas. Given ϒ= 1.4.
e) Derive an expression for Clausius- Clayperon equation.
3. a) Draw a T-S diagram of a Carnot cycle and derive an expression of efficiency of a heat engine working between T1 and T2.
b) A freezer operates between –15°C and 27°C. Calculate the maximum value of coefficient of performance (ω) for this refrigerator. With this ω, how much electrical energy would be required to freeze 0.8kg of water, initially at 0°C. Given specific latent heat of fusion = 334 kJ kg -1.
c) Using Maxwell’s relations, derive first and second TdS equations.
d) What is Joule-Thomson effect? Derive an expression of Joule-Thomson coefficient for a van der Waals’ gas.
4. a) The thermodynamic probability for a Boson system is given by
d) Derive an expression for survival equation for distribution of free paths. Also, plot survival equation.
e) Derive Einstein formula for mean square displacement of a Brownian particle.
2. a) Describe the construction and working of a Platinum resistance thermometer. Write its two principal merits.
b) Define the followings with example: (i) Intensive variables (ii) Extensive variables (iii) Adiabatic boundary (iv) Open system (v) Isolated system.
c) Obtain the expression for isothermal compressibility (βT) and coefficient of volume expansion (α) for a van der Waals’ gas.
d) Obtain an expression for work done by an ideal gas in an adiabatic process. Two litre of an ideal gas at a pressure of 5 atm expands adiabatically to two times its initial volume. Calculate the work done by the gas. Given ϒ= 1.4.
e) Derive an expression for Clausius- Clayperon equation.
3. a) Draw a T-S diagram of a Carnot cycle and derive an expression of efficiency of a heat engine working between T1 and T2.
b) A freezer operates between –15°C and 27°C. Calculate the maximum value of coefficient of performance (ω) for this refrigerator. With this ω, how much electrical energy would be required to freeze 0.8kg of water, initially at 0°C. Given specific latent heat of fusion = 334 kJ kg -1.
c) Using Maxwell’s relations, derive first and second TdS equations.
d) What is Joule-Thomson effect? Derive an expression of Joule-Thomson coefficient for a van der Waals’ gas.
4. a) The thermodynamic probability for a Boson system is given by
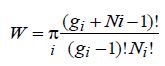 Using this relation, derive an expression for the Bose-Einstein distribution function.
b) Establish the Boltzmann relation S = kB ln W.
c) What is Gibbs paradox? Derive the Sackur-Tetrode equation for the entropy for an ideal monatomic gas.
d) The expression for Planck’s law for energy density is given by
Using this relation, derive an expression for the Bose-Einstein distribution function.
b) Establish the Boltzmann relation S = kB ln W.
c) What is Gibbs paradox? Derive the Sackur-Tetrode equation for the entropy for an ideal monatomic gas.
d) The expression for Planck’s law for energy density is given by
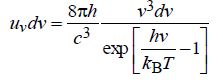 Using this expression, obtain (i) Wien’s law and (ii) Stefan-Boltzmann law.
Using this expression, obtain (i) Wien’s law and (ii) Stefan-Boltzmann law.To attend IGNOU PHE-06/BPHE-106 Term-End Examination, you must first submit your Assignments to the university and it is possible from the PHE-06/BPHE-106 study material. You can solve all necessary Assignments using Help Books. This will help in gaining good marks.
All best wishes with our efforts that you do not meet any obstacle before attending examinations next year. You can pass the B.Sc. Physics Programme Annual Exams with a good grade using Books/Materials from any one place at home or anywhere else!
ALL THE BEST!!!
Team GullyBaba