IGNOU MEC-03/MEC-103 - Quantitative Methods

IGNOU MEC-03/MEC-103 English Topics Covered

Block 1 - Introduction to Differential Calculus

• Unit 1 - Set Theory
• Unit 2 - Functions and their Graphical Representation
• Unit 3 - Differential Calculus: Functions, Limit and Continuity

Block 2 - Extreme Values and Optimisation

• Unit 1 - Maxima and Minima
• Unit 2 - Unconstrained Optimisation
• Unit 3 - Constrained Optimlsatlon

Block 3 - Integral Calculus and Economic Dynamics

• Unit 1 - Integration Techniques
• Unit 2 - Integration and Economic Dynamics
• Unit 3 - Difference Equations and Applications in Economic Dynamics

Block 4 - Matrices and Vectors

• Unit 1 - Vector Analysis
• Unit 2 - Linear Algebra
• Unit 3 - Input-Output Analysis
• Unit 4 - Linear Programming

Block 5 - Statistical Methods-I

• Unit 1 - Descriptive Statistics
• Unit 2 - Correlation and Regression Analysis
• Unit 3 - Probability Distribution
• Unit 4 - Probability Theory

Block 6 - Statistical Methods-II

• Unit 1 - Sampling Theory
• Unit 2 - Sampling Distributions
• Unit 3 - Statistical Inferences

IGNOU MEC-03/MEC-103 Hindi Topics Covered

Block 1 - अंतरक गणन विधि: विषय प्रवेश

• Unit 1 - फलां, सीमांत और सातत्य
• Unit 2 - अवकलज
• Unit 3 - आंशिक अवकलन

Block 2 - उभयान्त मान और इष्टतमीकरण

• Unit 1 - भूयिष्ठक एवं अल्पिष्ठक
• Unit 2 - अनिबाधित इष्टतमीकरण
• Unit 3 - निबाधित इष्टतमीकरण

Block 3 - समाकलन गणित और आर्थिक प्रावैगिकी

• Unit 1 - समाकलन और आर्थिक प्रावैगिकी में अनुप्रयोग
• Unit 2 - अंतर समीकरण और आर्थिक प्रावैगिकी में अनुप्रयोग

Block 4 - रैखिक बीजगणित एवं अर्थशास्त्रीय अनुप्रयोग

• Unit 1 - सदिश विश्लेषण
• Unit 2 - रैखिक बीजगणित
• Unit 3 - आगत-निर्गत विश्लेषण
• Unit 4 - रैखिक आयोजना

Block 5 - सांख्यिकीय विधियाँ-I

• Unit 1 - आँकड़ा प्रस्तुति और वर्णात्मक सांख्यिकी
• Unit 2 - सहसंबंध एवं समाश्रयन विश्लेषण
• Unit 3 - प्रायिकता सिद्धांत
• Unit 4 - प्रायिकता बंटन

Block 6 - सांख्यिकीय विधियाँ-II

• Unit 1 - न्यायदर्शन सिद्धांत
• Unit 2 - न्यायदर्शन बंटन
• Unit 3 - सांख्यिकीय अनुमिति

IGNOU MEC-03/MEC-103 (July 2024 - January 2025) Assignment Questions

Section A Answer the following questions in about 700 words each. The word limits do not apply in case of numerical questions. 1. a. Consider the following utility maximization problem, in which the utility function of the consumer is given by U(x,y)=x0.5y0.5. The consumer income is I=100 and px=2 and py=3. Find the utility maximizing x and y when the budget constraint of the consumer may or may not bind. (Apply Kuhn-Tucker method) b. Explain the theorem of second order optimum. 2. Given the input matrix and the final demand vector: a) Explain the economic meaning of the elements 0.33,0 and 200 b) Explain the economic meaning of (if any) of the third column sum c) Explain the economic meaning of (if any) of the third row sum d) Write out the specific input-output matrix equation for this model e) Find the solution output levels of the three industries using Cramer’s rule. Section B Answer the following questions in about 400 words each. The word limits do not apply in case of numerical questions. 3. Using Simplex method solve the problem: Maximise 𝜋 = 6𝑥1 + 2𝑥2 + 5𝑥3 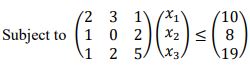x1, x2, x3 ≥ 0 4. a.) A salesman has 50% chance of making a sale. If two customers enter the shop, what is the probability that the salesman will make a sale? b.) If the events A and B are independent, then show that Ac, Bc, A and B are pair wise independent. 5. a) Discuss the nature of the following time path: 𝑦𝑡 = 3𝑡 + 1 b) Solve equation: 𝑦𝑡+1 −1/3𝑦𝑡 = 6 𝑓𝑜𝑟 𝑦0 = 1 6. Examine the following functions for maxima and minima: a) 𝑧 = 2𝑥2 + 𝑥𝑦 + 4𝑦2 + 𝑥𝑧 + 𝑧2 + 2 b) 𝑧 = 𝑒2𝑥 − 𝑒𝑦 + 𝑒2𝑧 − 2(𝑥 + 𝑒) + 𝑦 7. Write short notes on following: e) Euler’s theorem f) Riemann Sum g) Point of inflexion h) Chi square test of goodness of fit

IGNOU MEC-03/MEC-103 (July 2023 - January 2024) Assignment Questions

IGNOU MEC-03/MEC-103 (July 2024 - January 2025) Assignment Questions

खंड - क प्रत्येक प्रश्न का उत्तर लगभग 700 शब्दों में देना है। परिमाणात्मक प्रश्नों पर शब्द सीमा लागू नहीं होती । 1. (क) निम्नलिखित उपयोगिता अधिकतमकरण समस्या पर विचार करें, जिसमें उपभोक्ता का उपयोगिता कार्य U(x,y) = x 0.5 y0.5 द्वारा दिया गया है। उपभोक्ता आय I = 100 है और px = 3 । जब उपभोक्ता की बजट बाधा बाध्य हो भी सकती है और नहीं भी, तो x तथा y को अधिकतम करने वाली उपयोगिता ज्ञात कीजिए। (कुछ टकर विधि लागू करें) (ख) द्वितीय क्रम इष्टतम की प्रमेय की व्याख्या कीजिए । 2. इनपुट मैट्रिक्स और अंतिम मांग वेक्टर को देखते हुए: (क) 0.33.0 और 200 के अवयवों का आर्थिक अर्थ समझाइए (ख) तीसरे स्तंभ योग के (यदि कोई हो) का आर्थिक अर्थ समझाइए (ग) तीसरी पंक्ति के योग (यदि कोई हो) का आर्थिक अर्थ समझाइए (घ) इस मॉडल के लिए विशिष्ट इनपुट-आउटपुट मैट्रिक्स समीकरण लिखें (ड) क्रमर के नियम का उपयोग करके तीन उद्योगों के समाधान उत्पादन स्तर का पता लगाएं। खंड - ख प्रत्येक प्रश्न का उत्तर लगभग 500 शब्दों में देना है। परिमाणात्मक प्रश्नों पर शब्द सीमा लागू नहीं होती। 3. सरल (simplex) विधि का उपयोग करके समस्या का समाधान करे भूयिष्ठ बनाएं π = 6x1 + 2x2 + 5x3 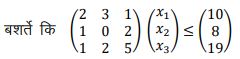और 𝑥1,𝑥2, 𝑥3 ≥ 0 4. (क) एक विक्रेता के पास बिक्री करने का 50% मौका है। यदि दो ग्राहक दुकान में प्रवेश करते हैं. तो विक्रेता द्वारा बिक्री किए जाने की प्रायिकता क्या है? (ख) यदि घटनाएं A और B स्वतंत्र हैं, तो दर्शाइए कि Ac, Bc, A और B युग्म वार स्वतंत्र हैं। 5. (क) निम्नलिखित समय पथ की प्रकृति पर चर्चा कीजिए: 𝑦𝑡 = 3 𝑡 + 1 (ख) समीकरण को हल करें: Yo=1 के लिए 𝑦𝑡+1 − 1/3 𝑦𝑡 = 6 6. नीचे दिए गए फलनों की भूयिष्ठकों अथवा अल्पिष्ठकों हेतु जांच कीजिए: (क) z= 2𝑥 2 +𝑥𝑦 + 4𝑦 2 + 𝑥𝑧 + 𝑧 2 + 2 (ख) z= 𝑒 2𝑥 − 𝑒 𝑦 + 𝑒 2𝑧 − 2(𝑥 + 𝑒) + 𝑦 7. निम्नलिखित पर संक्षिप्त टिप्पणीयाँ लिखिए: (क) यूलर प्रमेय (ख) रीमन संकलन (Riemann Sum ) (ग) नीति परिवर्तन बिंदु (Inflexion Point) (घ) उपयुक्तता के गुण की काई-वर्ग जाँच (Chi square Test of goodness of Fit )

IGNOU MEC-03/MEC-103 (July 2023 - January 2024) Assignment Questions

Related Codes