Bought By: 8097
Rating: 3.7

Get Good Marks in your B.Sc. Mathematics Programme in the Term-End Exams even if you are busy in your job or profession.
We've sold over 64,721,966 Help Books and Delivered 81,707,707 Assignments Since 2002.
As our customers will tell you...yes, it really result-oriented.







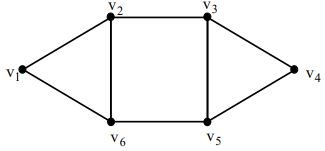 b) Is the complement of the Peterson graph planar? Justify your answer.
c) What do you understand by a subdivision of a graph? Is every subdivision of a Hamiltonian graph Hamiltonian? Justify.
5. a) Let 𝐶𝑛 denote the number of 𝑛-tuples whose entries are 0 or 1 only, and two consecutive entries of which are zero.
i) Find 𝐶1 and 𝐶2.
ii) Find a recurrence relation for 𝐶𝑛.
b) write down and count all the partitions of the number 7. To verify your answer use the generating function for Pn, taking n = 7 in Theorem 5 (of Unit 5, Block2).
6. a) Express x5 in terms of falling factorials and hence evaluate
b) Is the complement of the Peterson graph planar? Justify your answer.
c) What do you understand by a subdivision of a graph? Is every subdivision of a Hamiltonian graph Hamiltonian? Justify.
5. a) Let 𝐶𝑛 denote the number of 𝑛-tuples whose entries are 0 or 1 only, and two consecutive entries of which are zero.
i) Find 𝐶1 and 𝐶2.
ii) Find a recurrence relation for 𝐶𝑛.
b) write down and count all the partitions of the number 7. To verify your answer use the generating function for Pn, taking n = 7 in Theorem 5 (of Unit 5, Block2).
6. a) Express x5 in terms of falling factorials and hence evaluate 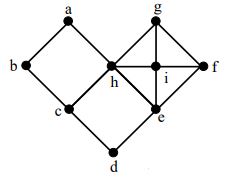 c) How many numbers from 0 to 759 are not divisible by either 3 or 7?
8. a) Solve the recurrence relation:
an = 2an-1 + 1 if n ≥ 1 and a0 = 0,
using generating function technique. Also find a5 using your answer.
b) Is there a 4-regular graph on 7 vertices? Justify your answer.
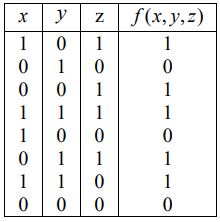
c) Find the Boolean expression in the DNF form for the function defined in tabular form below:
c) How many numbers from 0 to 759 are not divisible by either 3 or 7?
8. a) Solve the recurrence relation:
an = 2an-1 + 1 if n ≥ 1 and a0 = 0,
using generating function technique. Also find a5 using your answer.
b) Is there a 4-regular graph on 7 vertices? Justify your answer.
c) Find the Boolean expression in the DNF form for the function defined in tabular form below:
To attend IGNOU MTE-13 Term-End Examination, you must first submit your Assignments to the university and it is possible from the MTE-13 study material. You can solve all necessary Assignments using Help Books. This will help in gaining good marks.
All best wishes with our efforts that you do not meet any obstacle before attending examinations next year. You can pass the B.Sc. Mathematics Programme Annual Exams with a good grade using Books/Materials from any one place at home or anywhere else!
ALL THE BEST!!!
Team GullyBaba