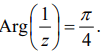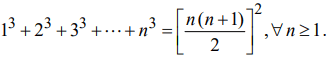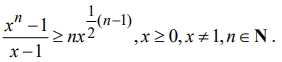IGNOU MTE-04 Elementary Algebra - IGNOU Solved Assignment (Latest)
Get IGNOU MTE-04 Assignments Soft Copy ready for Download in PDF for (January 2024 – December 2024) in English Language.
- Helps save time and effort-really well
- Promises Good Marks in Less Time
- Answers that are verified and accurate
- Based on IGNOU Guidelines.
BUY MTE-04 COMBO and Save upto 50%
- Description
- Previous Year Solved Question Papers Included
- Assignments Details
- Assignment Submission End Date
- What's Included
PLEASE MATCH YOUR ASSIGNMENT QUESTIONS ACCORDING TO YOUR SESSION
MTE-04 (January 2023 – December 2023) Assignment Questions



IGNOU MTE-04 (January 2022 – December 2022) Assignment Questions
1) Which of the following statements are true? Justify your answers. (This means that if you think a statement is false, give a short proof or an example that shows it is false. If it is true, give a short proof for saying so.
i) The system of equations 2x + 6y + z = 2, x + ky + 3z = 4 has a unique solution for some value of k .
ii) Any polynomial equation with real coefficients has at least one real root.
iii) If A and B are two sets, then .
iv) There is one and only one complex cube root of 1.
v) The arithmetic mean of 3 non-zero real numbers is greater than their harmonic mean.
vi) Any pair of linear equations in two variables is consistent.
vii) If f(x) = 0 is a polynomial equation of degree n over R, then it must have at least n distinct roots in R .
viii) A system of linear equations that cannot be solved by Cramer’s rule be inconsistent.
ix)
x) If z = -1 + i , then
2) a) Check if the equations can be solved by Cramer’s rule. If it can be, then apply the rule for solving the equations; otherwise solve it by the method of Gaussian elimination.
-x + 3z = 2,
2x + y – 4z- = -1
x + 2y + z = 4.
b) A concert hall has 400 seats. These seats are divided into two sections A and B. The cost of a ticket in Section A is Rs. 155 and that in Section B is Rs. 105. Assuming that all the seats are occupied, determine the number of seats allocated to each section so as to get a daily revenue of Rs. 50,000/-.
c) Solve the equation:
x4 – 10×3 + 42×2 – 82x + 65 = 0, given that the product of two of its roots is 13.
3) a) Verify De Morgan’s laws for the sets A = {5, 3, -1}, B = {-5, -3, -1}.
b) Can you solve the following system of equations by Cramer’s rule? If so, solve it using this rule. If not, solve the given system of equations by elimination method.
x + 2y + 3z = 2
2x + 3y = 5
3x + 6y + 9z = 6
c) Show, by induction, that
d) Find the number of distinct solutions of 2x – 3y = 7, x, y, < 0
4) a) For z1 = 3 + 4i and z2 = 4 – 3i, write in polar and exponential form, and represent
and z1 / z2 in an Argand diagram.
b) For
c) If we know that the roots of the cubic equations x3 – 61×2 – 8000 = 0 are in G.P., then find the roots of the equation.
5) a) Find the roots of the equation
g(x) = x4 + 7×3 + 11×2 + 7x + 10 = 0.
Given that (x2 + 1) divides g(x).
b) Obtain the solution set of the linear system given below, by the Elimination method:
x + 4y + 5z = 4
3x + 2y + 6z = 2
10y + 9z = 10
c) Prove that
6) a) Prove that, by the principle of mathematical induction,
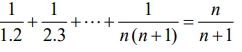
b) Akhila enjoyed two types of games, type A and type B, at the village fair. Each time she played type A, it cost ` 3 and each time she played type B, it cost ` 4. If the number of B games played was half the number of type A games played by her, and the total amount spent was ` 20, write a system of linear equations for the problem of finding the number of times she played each type of game.
c) Given an example, with justification, of each of the following:
(i) An element of (C x Q) / (Q x C);
(ii) An infinite set whose complement in R is infinite.
7) a) Find the roots of the polynomial equation
given that two of its roots are equal to 3.
b) Use the principle of mathematical induction to show that for any positive integer
c) A coach buys 3 cricket bats and 6 balls for ` 3,900. Later, he buys 1 bat and 3 balls for another team for ` 1,450. Write two linear equations to represent the purchases. Why can the linear system so obtained be solved by Cramer’s rule? Also, use the rule to solve the system, and interpret the solution in the given context.
8) a) Use Cardano’s method to obtain the roots of x3 – 3x + 2 = 0.
b) Show that
9) a) If A, B are any two sets, then state the conditions under which A x B = B x A. Justify your conditions.
b) Obtain the resolvent cubic of x4 + 5×3 – 10x +2 = 0, according to Ferrari’s method.
c) Give a real life situation problem, which is mathematically translated into
2x + y + 2z = 18, x + 3y + 3z = 24, 3y = 6
Also, explain how this linear system models your problem.
MTE-04 Assignments Details
| University | : | IGNOU (Indira Gandhi National Open University) |
| Title | : | Elementary Algebra |
| Language(s) | : | English |
| Code | : | MTE-04 |
| Degree | : | |
| Subject | : | Mathematics |
| Course | : | Core Courses (CC) |
| Author | : | Gullybaba.com Panel |
| Publisher | : | Gullybaba Publishing House Pvt. Ltd. |