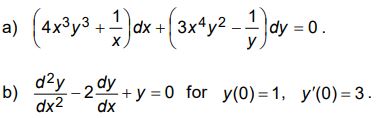IGNOU BPHCT-131 Mechanics - Latest Solved Assignment

PART A

1. a) Determine the projection of whereand 

b) Obtain the derivative and unit tangent vector at t = 1 for a vector function

2. Solve the following ordinary differential equations:

3. a) A mass of 10 kg, is released from rest on an incline that makes a 30° angle with the horizontal. In 2 s, the mass is observed to have moved a distance of 4 m. What is the coefficient of kinetic friction between the mass and the surface of the incline? Draw the free body diagram.

b) A ball of mass 0.5 kg collides with a wall at a speed of 15.0 ms-1 and bounces back with a speed of 12.5 ms-1. If the average force exerted by the ball is 1100 N calculate the impulse and the time for which the collision lasted.

c) A box of mass 8 kg slides at a speed of 10 ms-1 across a smooth level floor before it encounters a rough patch of length 3.0 m. The frictional force on the box due to this part of the floor is 70 N. What is the speed of the box when it leaves this rough surface? What length of the rough surface would bring the box completely to rest?

PART B

4. a) A cylindrical drum has a radius of 0.45 m and is initially at rest. It is then given an angular acceleration of 0.40 rad s-2. At time t = 8.0 s calculate (i) the angular speed of the drum, (ii) the centripetal acceleration of a point on the rim of the drum, (iii) the tangential acceleration at that point, and (iv) the resultant acceleration at that point.

b) The distance between the oxygen molecule and each of the hydrogen atoms in a water (H2O) molecule is 0.96 Å and the angle between the two oxygen-hydrogen bonds is 105°. Treating the atoms as particles, find the centre of mass of the system.

c) The planet earth is 1.5 × 1011m from the sun and orbits the sun in one year. The planet Pluto takes 248 years to orbit the sun. How far is Pluto from the sun?

d) A 1400 kg car moving south at 11 ms-1 is struck by a 1800 kg car moving east at 30 ms-1. The cars are stuck together. How fast and in what direction do they move immediately after the collision? (2016)

5. a) The oscillation of a simple harmonic oscillator is described by the equation
x(t) =0.6 sin(0.2t + 0.8) m
where t is expressed in seconds. Determine the amplitude, time-period and frequency of oscillation, maximum velocity, maximum acceleration and initial displacement of the oscillator.

b) The following two orthogonal oscillations act on a body simultaneously:

Determine the path of resultant motion of the body.

c) A damped harmonic oscillator has a first amplitude of 30 cm. The amplitude reduces to 3 cm after 100 oscillations. If the period of damping is 9.2s calculate the logarithmic decrement and damping factor. Also determine the number of oscillations in which the amplitude drops by 50 percent.

d) A progressive transverse wave is given by y(x,t) = 0.06 sin(1256t + 31.4x) m , where t is in seconds. Determine the direction of propagation of the wave and calculate its amplitude, wavelength, frequency and velocity.