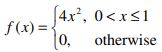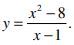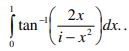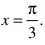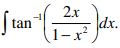IGNOU MTE-03 Mathematical Methods - IGNOU Solved Assignment (Latest)
Get IGNOU MTE-03 Assignments Soft Copy ready for Download in PDF for (January 2024 – December 2024) in English Language.
- Helps save time and effort-really well
- Promises Good Marks in Less Time
- Answers that are verified and accurate
- Based on IGNOU Guidelines.
BUY MTE-03 COMBO and Save upto 50%
- Description
- Previous Year Solved Question Papers Included
- Assignments Details
- Assignment Submission End Date
- What's Included
PLEASE MATCH YOUR ASSIGNMENT QUESTIONS ACCORDING TO YOUR SESSION
MTE-03 (January 2024 – December 2024) Assignment Questions
1. State whether the following statements are true or false giving reasons in support of your answer.
i) A binomial distribution has mean 3 and variance 4.
ii) The function f (x) = x3 has no maxima or minima.
iii) The line of regression of x on y is the same as the line of regression of y on x.
iv) The plane x + 2y − z = 5 is parallel to the line
v) A continuous random variable can have probability density function
2. a) Define Is f injective, surjective, monotone?
b) A bag contains 3 white balls and 2 red balls. Another bag contains 5 white and 3 red balls. A bag is chosen at random and a ball is drawn from it. Find the probability that it is white.
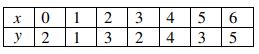
c) Compute the correlation co-efficient between X and Y for the following data:
3. a) Find asymptotes of the graph of the function
b) Find the term independent of a in the binomial expansion of
c) In a certain Poisson distribution the probability of 3 successes is exactly equal to the probability of 4 successes. Find its mean and standard deviation. Also find the probability of more than 1 success for the given distribution.
4. a) Integrate
b) Find the mean and the standard deviation of a random variable with the following probability density function:
c) A club has 9 member having ages 21, 28, 23, 29, 52, 43, 32, 37 and 30 years. One has to be at least 30 years of age to be eligible for the presidentship of the club. A simple random sample of size 5 is selected to provide an estimate of the population proportion eligible for presidentship. Find the mean and the standard error of this estimate
5. a) Find the radius of the sphere which passes through the points (0,0,1) , (1,0,0), (0,1,0) and (0,0,1).
b) Verify Euler’s theorem for the function
c) Two groups of 10 plants each were grown on two different fertilizers. The average height of first group of plants was 92.44 cm, with a standard deviation of 4 cm. For the second group, the average height was 90 cm with a standard deviation of 2 cm. At 5% level of significance test the hypothesis that first fertilizer is better than the second in terms of the plant growth
[Given t 0.05, 18= 1.734, t 0.05, 20 =1.729 t 0.05, 22 =1.721]
6. a) Find (a × b)⋅ c where
a = 2i + 3 j − k, b = i − 2 j + k, c = 3i + 4 j + 5k.
b) Solve the differential equation
c) A garden pea plant is genetically mixed for the gene pair Tt, where the gene T (for tall) is dominant over the gene t (for short). The plant produced 40 tall and 20 short offspring. Using 2 χ -test find out whether the plant was self fertilized or fertilized by a short plant at 5% level of significance
7. a) It is known that 10 men out of every 100 men and 30 women out of every 1000 women are color blind. In a community, half the population is male. Using Baye’s theorem find the probability that a color blind person chosen at random from among all color blind persons in the community is male.
b) Show that sin x (1 + cos x) has a maximum at
c) Find the sum of the first n terms of the series log 2 + log6 + log18 + log54 + …. .
8. a) If f : R → R is defined by f (x) = 4x +1 then show that f is a bijection. Find the formula that defines f-1.
b) Obtain
c) The difference of mean and variance of a binomial distribution of 9 trails is 4. Find the probability p of success of the binomial distribution. Also find the probability of (i) exactly two successes and (ii) less than 2 successes.
9. a) A and B are two events which are independent. The probability that both A and B occur is 1/6 and the probability that neither of them occurs is 1/3. Find the probability of the occurrences of A and B.
b) If , y = ex + e−x, prove that √y2−4
c) Fit a straight line for regression of Y on X from the following table.
Find the value of y when x = 10.
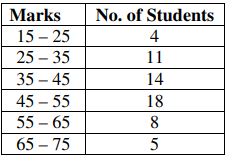
10. a) Calculate: (i) Quartile deviation and (ii) Mean Deviation from mean for the following data:
b) Find two positive numbers x and y such that x + y = 60 and xy3 is maximum
c) Find the angle between the planes 6x − 4y + 2z =1 and 3x +12y − 9z = 2. Also specify the type of the angle obtained.
IGNOU MTE-03 (January 2023 – December 2023) Assignment Questions





MTE-03 Assignments Details
| University | : | IGNOU (Indira Gandhi National Open University) |
| Title | : | Mathematical Methods |
| Language(s) | : | English |
| Code | : | MTE-03 |
| Degree | : | |
| Subject | : | Mathematics |
| Course | : | Core Courses (CC) |
| Author | : | Gullybaba.com Panel |
| Publisher | : | Gullybaba Publishing House Pvt. Ltd. |