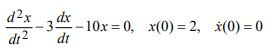Name: Mathematical Methods in Physics-II
SKU: 14769
Availability: InStock

IGNOU PHE-05 Mathematical Methods in Physics-II - Latest Solved Assignment

Sale!

#1 Best Selling IGNOU Solved Assignments in All Study Guides

Get IGNOU PHE-05 Assignments Soft Copy ready for Download in PDF for (January 2024 – December 2024) in English Language.

Helps save time and effort-really well
Promises Good Marks in Less Time
Answers that are verified and accurate
Based on IGNOU Guidelines.

Know More..

Type

Select Medium

Session

~~₹200.00~~₹100.00

Save ₹100.00 (50%)

Buy on WhatsApp

Also Buy Your Help Book or Bulk Assignments

Buy PHE-05 Help Book Buy Bulk Assignments (Soft or Hard) Copy

SKU: N/A Categories: B.Sc., IGNOU Solved Assignments

BUY PHE-05 COMBO and Save upto 50%

BPHE-101/PHE-01

BPHE-102

BPHE-104/PHE-04

PHE-05

PHE-06/BPHE-106

Language :

English

Semester :

1st

2nd

Year :

1st

₹700.00

~~₹1,400.00~~

Save ₹700.00

Add This Combo View Details

View More Combos

IGNOU - PHE-05 (Jan 23 - Dec 23, Jan 24 - Dec 24) Solved Assignment

Are you looking to download a PDF soft copy of the Solved Assignment PHE-05 - Mathematical Methods in Physics-II? Then GullyBaba is the right place for you. We have the Assignment available in English language. This particular Assignment references the syllabus chosen for the subject of Physics, for the January 2024 - December 2024 session. The code for the assignment is PHE-05 and it is often used by students who are enrolled in the B.Sc. Degree. Once students have paid for the Assignment, they can Instantly Download to their PC, Laptop or Mobile Devices in soft copy as a PDF format. After studying the contents of this Assignment, students will have a better grasp of the subject and will be able to prepare for their upcoming tests.

PLEASE MATCH YOUR ASSIGNMENT QUESTIONS ACCORDING TO YOUR SESSION

PHE-05 (January 2024 – December 2024) Assignment Questions

IGNOU PHE-05 (January 2023 – December 2023) Assignment Questions

1. a) Solve the following ordinary differential equations:
i) y’ = (y -1) cot x
ii) y” + 2y’ + y = e- 2x
b) Solve the initial value problem:

2. A parachutist is falling with a speed of 100 ms-1 when his parachute opens. If the air resistance is (Mv2)/ 25 where M is the total mass of the man and his parachute, find the speed of the man as a function of time t after the parachute opens. Take g = 10 ms-1.

3. A 1 kg mass is attached to a spring of spring constant 12 Nm-1 and the system is immersed in a medium which exerts a damping force equal to 8 times the instantaneous velocity of the mass. Determine the position of the mass as a function of time if it is released from rest at a point 0.5 m below its equilibrium position.

4. Determine the roots of the indicial equation around the point x = 0 for the following ODE:

5. a) Show that:

is a solution of the one-dimensional heat equation.
b) Determine all the first and second order partial derivatives for the function:
u (x, y)= x2 sin y + y2 cos x

6. Write the following partial differential equation in spherical polar coordinates and reduce it to a set of three ODEs by the method of separation of variables:
∇2 f + k2 f = 0

7. Obtain the Fourier series for the following odd function which has a period of 2π:
f(x)= x sin 2 x for – π < x < π

8. Solve the heat conduction problem:

Given that
T (0,t) = T (5,t) = 0
and
T (x,0) = 3sin(πx) – 2sin(2πx) + sin(5πx)

PHE-05 Assignments Details

University	:	IGNOU (Indira Gandhi National Open University)
Title	:	Mathematical Methods in Physics-II
Language(s)	:	English
Code	:	PHE-05
Degree	:	B.Sc.
Subject	:	Physics
Course	:	Core Courses (CC)
Author	:	Gullybaba.com Panel
Publisher	:	Gullybaba Publishing House Pvt. Ltd.