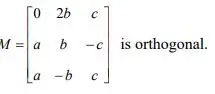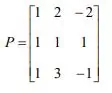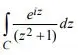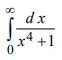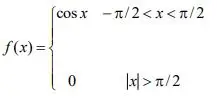PLEASE MATCH YOUR ASSIGNMENT QUESTIONS ACCORDING TO YOUR SESSION
IGNOU PHE-14 (January 2024 – December 2024) Assignment Questions
IGNOU PHE-14 (January 2023 – December 2023) Assignment Questions
1. a) Determine the values of a, b, c when
b) Verify the Cayley-Hamilton theorem of the matrix.
and hence obtain. P-1.
c) If Aij is an antisymmetric tensor and Bi is a vector, show that Aij Bi Bj = 0.
d) What are the four conditions to be satisfied by the elements of a group? Show that the set of all complex numbers of unit magnitude u(1) ={z : |z|=1} forms a group.
2. a) Using the method of residues, evaluate the contour integral
where C is defined by | z | < 4.
b) Using the method of residues, evaluate the integral
c) i) Show that the function f (z) = z3 is analytic in the entire z-plane.
ii) Obtain the Taylor series expansion of cos2 z about z = 0.
3. a) Obtain the Fourier cosine transforms of the function:
b) Calculate the inverse Laplace transform of the function:
c) Solve the initial value problem using the method of Laplace transforms:
y’’ – 2y’ – 3y = 0; y(0)= 1, y’(0) = 7
d) Calculate the Laplace transform of t n e at.
4. a) Show that
b) Using the generating function
for Legendre polynomials show that:
c) Use Rodrigues’ formula for Laguerre polynomials to generate L4(x).