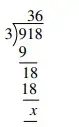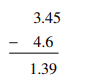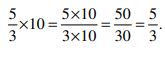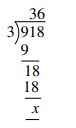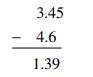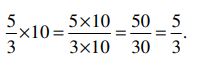PLEASE MATCH YOUR ASSIGNMENT QUESTIONS ACCORDING TO YOUR SESSION
IGNOU AMT-01 (July 2024 – June 2025) Assignment Questions
IGNOU AMT-01 (July 2023 – June 2024) Assignment Questions
1. Which of the following statements are true? Give reasons for your answers.
a) Usually the first experience of subtraction that a child has is in Class I.
b) Primary school children of any age continue to feel the need to use concrete aids for learning.
c) Learning algebra helps the child to develop mathematical thinking.
d) Children don’t get an opportunity to apply their knowledge of negative numbers till they reach class 10.
e) The language of mathematics is made up of the terminology and symbols used in mathematics.
2. a) List at least 5 ways in which a farmer uses mathematics while farming, clearly mentioning what are areas of mathematics involved are.
b) What are the advantages of using algorithms? What are the dangers that we must watch out for while illustrates them in the context of multiplication algorithm for multiplying two decimal fractions.
3. In the block you have read that cognitive development is continuous and there are phases within each stage. Give two examples, one from the unit and one new example, to explain what this means. You should justify and explain both your examples in about 150 words each.
4. a) What is the difference between repetition and rote-learning? Illustrate your answer by giving an example from addition of natural numbers.
b) Give an example each (apart from the ones in the blocks) to show
i) the difference in the meaning of ‘angles’ in English and in mathematics,
ii) how the language of algebra helps us to express statements briefly and concisely.
5. Write down an activity each, different from those given in the blocks, to help children realise that
i) − (−n) = n, for any number n?
ii) division by zero is not meaningless?
6. When a child was asked to solve 5/3 X 10, she wrote
i) Why do you think she made this error?
ii) How would you help her to apply the operation correctly?
7. a) Suggest one game in which the children are simultaneously asked to estimate the measure the size of an object and an angle. Justify your choice of the game.
b) “Children learn by experiencing things”. Justify this statement by giving two examples, one pertaining to learning fractions and the other pertaining to learning about shapes.
8. a) Do you think that the number-line is a useful tool in teaching the operation of addition and subtraction of fractions? Justify your answer.
b) Suggest a teaching method or an activity to bring out the difference between volume and capacity?
9. Write down a details plan (See Unit 4) for teaching children of class 6 the concept of variable.
10. a) Write “11” in base 2. Show the steps you used for doing this.
b) Explain E-L-P-S sequence of learning. Illustrate it in the context of learning the concept of “Time”.
c) Give two distinct that are equivalent to 3/7. Pictorially explain how they are different.
IGNOU AMT-01 (July 2024 – June 2025) Assignment Questions
1. क) प्राइमरी स्तर पर गणित पढ़ने-पढ़ाने में मूर्त सामग्री और व्यावहारिक अनुभवों का प्रयोग क्यों ज्यादा प्रभावी होता है, वर्णन कीजिए प्रत्येक को एक-एक उदाहरण की सहायता से इसे स्पष्ट कीजिए ।
ख) जया ने भाग के सवाल को निम्नलिखित तरीके से हल कियाः
i) उसने क्या गलती की?
ii) उसकी इस गलती का संभावित कारण क्या है?
iii) उसकी इस गलत धारणा को दूर करने के लिए एक कार्यनीति तैयार कीजिए ।
2. क) निम्नलिखित प्रत्येक के लिए रोज़मर्रा की ज़िन्दगी से ऐसी दो परिस्थितियाँ बताइए जिनमें हम हम इनका प्रयोग करते हैं:
i) ज्यामिति
ii) पूर्णाक
(iii) बीजगणित
ख) मुक्तांत प्रश्न (open-ended) क्या होता है? ऐसे प्रश्नों के दो उदाहरण दीजिए। इनमें से एक उदाहरण एक अंक वाली संख्या के जोड़ से और एक उदाहरण गुणा से संबंधित होना चाहिए।
3. क) आठ वर्ष की मीरा का जन्मदिन दिसम्बर में होता है और रिंकू (6 वर्षीय) का जन्मदिन अप्रैल में है। रिंकू का कहना है कि रिंकू उससे बड़ा है। रिंकू को यह गलतफहमी क्यों है? रिंकू की इस गलतफहमी को दूर करने में रिंकू की मदद करने के लिए एक विस्तृत कार्यनीति तैयार कीजिए ।
ख) निम्नलिखित की चित्रात्मक प्रस्तुति दीजिए:
i) .17 3.07
4. क) गणित किस प्रकार एक भाषा है, स्पष्ट कीजिए। दो ऐसी अलग-अलग गतिविधियाँ बताइए जिनसे यह आकलन करने में मदद मिल सके कि उसकी भाषा के साथ बच्चों कितनी सहज हो पायी।
ख) निम्नलिखित प्रत्येक स्थिति का एक ऐसा पुष्टियुक्त उदाहरण दीजिए जिसमें बच्ची निगमनिक सोच का प्रयोग करती है।
i) खेलते हुए
ii) गणित में।
ग) एक उचित उदाहरण की सहायता से अंकगणित और बीजगणित के बीच संबंध स्पष्ट कीजिए ।
5. क) सुमन फुटबाल खेलता है। इसके लिए वह जिन गणितीय अवधारणाओं का प्रयोग करता है, उनमें से दो अलग-अलग अवधारणाएँ बताइए। अपने उत्तर की पुष्टि कीजिए ।
ख) ‘गणित सोपानक्रमिक प्रकृति का है। दो उदाहरणों की सहायता से इस कथन की पुष्टि कीजिए ।
ग) दो ऐसी भिन्न प्रकार की गतिविधियाँ सुझाइए जो से.मी. को मीटर से संबद्धित करने के लिए एक फार्मूले तक पहुँचने में बच्चों की मदद कर सकें।
6. क) मूल्यांकन के प्रत्येक चरण में तत्काल फीडबैक (प्रतिपुष्टि) के माध्यम से मूल्यांकन करना सिखाने- सीखने की प्रक्रिया का हिस्सा होना चाहिए। स्थानीय मान सिखाने व सीखने के प्रत्येक चरण के संदर्भ में इस कथन को स्पष्ट कीजिए। इसके आगे दिए गए संदर्भ (स्थानीय मान) में मूल्यांकन के लिए तीन अलग-अलग बहु आकलन तकनीकें बताइए ।
ख) एक बच्ची को आप कैसे यकीन दिलायेंगे कि किसी भी संख्या को 0 से गुणा करने पर उत्तर 0 होता है।
7. क) “भिन्न” की अवधारणा सीखने के संदर्भ में निम्नलिखित प्रत्येक का प्रयोग उदाहरण देते हुए स्पष्ट कीजिए
i) एक बाहरी गतिविधि
ii) अखबार और मैगजीनें (पत्रिकाएँ)
ख) एक बच्ची द्वारा नीचे की गई घटा के पीछे क्या संभव सोच है?
क्या यह दर्शाता है कि बच्ची संख्याओं की घटा करने की प्रक्रिया नहीं समझ पायी है। अपने उत्तर के कारण बताइए। उसकी गलती को ठीक करने में आप उसकी मदद कैसे करेंगे?
8. क) i) ‘समीकरण’ क्या है? क्या सभी समीकरणों में चर शामिल होता है? एक ऐसे समीकरण का उदाहरण दीजिए जिसमें चर हो और जो समान न हो।
ii) आइए एक संख्या- खेल पर विचार करें। एक संख्या सोचिए, उसे दुगुना करें उसे योग में छह जोड़ें, इस योग को आधे से विभाजित करें, फिर उसमें से तीन घटाएं आपको क्या उत्तर मिला? क्या आपको वही संख्या मिल गयी जो आपने पहले सोचा था ? क्यों? पुष्टि कीजिए ।
ख) सिद्ध कीजिए कि पहली n सम संख्याओं का योग सम संख्या होता है। क्या इसको सिद्ध करने का तर्क आगमनिक है, निगमनिक है या दोनों? अपने उत्तर की पुष्टि कीजिए ।
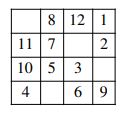
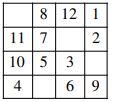
9. क) जादुई वर्ग क्या है? नीचे दिए वर्ग की प्रविष्टियाँ पूरी कीजिए और उसको जादुई वर्ग बनाइए ।
प्रविष्टियों को भरने के लिए इस्तेमाल की गई विधियें / तरीकों को स्पष्ट कीजिए। यह भी वर्णन कीजिए कि वह विधि क्यों कारगर है?
ख) अधिकांश गणित शिक्षण वास्तव में बच्चों को उन पैटनों के लिए ज्यादा जागरूक (जानकार) बनाने के लिए प्रोत्साहित करना, जिन्हें वे ढूंढते हैं और अपनी समझ (सोच) में उनका प्रयोग करते हैं। नीचे प्रश्न (i), (ii) और (iii) में दिए गए प्रश्नों को उत्तर देकर आप इस बात को स्पष्ट कर सकते हैं।
“कक्षा 5 की गणित की शिक्षिका ने कक्षा में निम्नलिखित पैटर्न दिखायाः
46×44 = 2024
63×67 = 4221
71×79 = 4909
उसने विद्यार्थियों को पैटर्न की पहचान करने के लिए कहा। थोड़ी देर बाद उसने विद्यार्थियों को “84 × 86” का उत्तर देने के लिए कहा। एक विद्यार्थी ने उत्तर दिया 7224.
i) विद्यार्थी द्वारा प्रयुक्त पैटर्न का पता लगाइए।
ii) बताइए यह क्यों कारगर है?
iii) यह गणितीय सोच को प्रोत्साहित करने में कैसे मदद करता है, वर्णन कीजिए ।
10. निम्नलिखित में से कौन से कथन सत्य है और कौन से असत्य? अपने उत्तर के कारण बताइएः
i) आज दिन उज्जवल है’ एक कथन है।
ii) पेंटागॉन के भीतरी कोणों का योग 450° होता है।
iii) पूर्व-संक्रियात्मक सोच दो वर्ष के उम्र की बच्ची की विशेषता है।
iv) यदि त्रिविमीय वस्तुओं की धारिता बढ़ती है तो उसका आयतन भी बढ़ जाता है।
v) प्रत्येक गणितीय सवाल का एक अद्वितीय हल होता है।
IGNOU AMT-01 (July 2023 – June 2024) Assignment Questions
1. निम्नलिखित में कौन से कथन सही हैं? अपने उत्तरों के कारण भी दीजिए।
क) घटाने का पहला अनुभव बच्चे को प्रायः कक्षा 1 में होता है।
ख) प्राइमरी स्कूल के किसी भी उम्र के बच्चों को सीखने में ठोस चीज़ों की सहायता की ज़रूरत बनी रहती है।
ग) बीजगणित सीखने से बच्चे को गणितीय सोच विकसित करने में मदद मिलती है।
घ) कक्षा 10 से पहले बच्चों को ऋणात्मक संख्याओं के अपने ज्ञान के उपयोग का अवसर नहीं मिलता ।
ड) गणित की भाषा, गणित में इस्तेमाल होने वाली शब्दावली तथा प्रतीकों से बनी है।
2. क) कम से कम पांच ऐसे उदाहरण दीजिए जहां किसान अपनी खेती-बाड़ी में गणित का उपयोग करते हों। हर उदाहरण में यह भी स्पष्ट कीजिए कि उसमें गणित की किन शाखाओं का उपयोग होता है।
ख) एल्गोरिद्मों को इस्तेमाल करने के क्या लाभ हैं? बच्चों को ऐल्गोरिद्म सिखाते समय हमें किन खतरों के प्रति सतर्क रहना चाहिए?
3. खण्ड में आप पढ़ चुके हैं कि संज्ञानात्मक विकास निरन्तर प्रक्रिया है और हर अवस्था में विभिन्न चरण होते हैं। इस बात को समझाने के लिए पुष्टि सहित दो उदाहरण दीजिए। एक उदाहरण इकाई से तथा एक उदाहरण नया हो। हर उदाहरण की व्याख्या लगभग 150 शब्दों में कीजिए ।
4. क) दोहराव और रटने में क्या फर्क है? अपनी बात को दो उदाहरणों की मदद से स्पष्ट कीजिए ।
ख) निम्नलिखित बातें समझाने के लिए खंडों में दिए गए उदाहरणों से हटकर एक-एक उदाहरण दीजिए ।
i) हिन्दी और गणित में ‘व्यापक तौर से के अर्थ में फर्क
ii) बीजगणित की भाषा किस तरह से कथनों को संक्षिप्त व सार रूप में व्यक्त करने में मदद देती है।
5. निम्नलिखित समझने में मदद के लिए, खंडों में दिए गए गतिविधियों से हटकर एक-एक गतिविधि दीजिए ।
i) किसी भी संख्या n के लिए – (n) = n होता है।
ii) शून्य से भाग देना निरर्थक है।
6. एक बच्ची से 5/3 x 10 हल करने को कहा गया। उसने लिखा
i) आपके ख्याल से उसने यह गलती क्यों की?
ii) सवाल को सही ढंग से करने में आप उसकी मदद कैसे करेंगे?
7. क) एक ऐसा खेल सुझाइए जिसमें बच्चों से किसी चीज़ के साइज़ या कोण या अवधि के माप का साथ-साथ अनुमान लगाने को कहा जाए।
ख) “बच्चे ठोस वस्तुओं के साथ अनुभव करके सीखते हैं।” दो उदाहरण देते हुए इस कथन की पुष्टि कीजिए। इनमें से एक उदाहरण भिन्न सीखने और एक आकारों के बारे में सीखने से संबंधित होना चाहिए।
8. क) क्या आपके विचार से संख्या रेखा, भिन्न का जोड़ व घटाव सिखाने का उपयोगी साधन हो सकती है ? उत्तर की पुष्टि कीजिए ।
ख) आयतन व धारिता की अवधारणाओं के बीच अंतर समझाने के लिए शिक्षण विधि या गतिविधि सुझाइए ।
9. कक्षा ‘6’ के बच्चों को चर की अवधारणा सिखाने के लिए एक विस्तृत योजना लिखिए ( इकाई 4 देखिए ) ।
10. क) आधार ‘2’ में ’11’ को लिखिए। ऐसा करने के लिए आपने जिन चरणों का प्रयोग किया है, उसे दर्शाइए ।
ख) सीखने की आ – भा-चि-प्र के क्रम का वर्णन कीजिए । कोणों के बारे में सिखाने के संदर्भ में इसे स्पष्ट कीजिए ।
ग) अलग–अलग भिन्ने बताइए जो 2/5के तुल्य हो। ये भी कैसे तुल्य है, इसे चित्र द्वारा स्पष्ट कीजिए ।