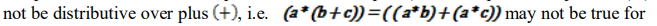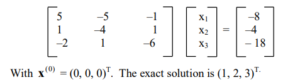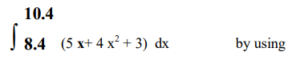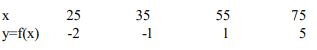PLEASE MATCH YOUR ASSIGNMENT QUESTIONS ACCORDING TO YOUR SESSION
IGNOU BCS-54 (July 2024 – January 2025) Assignment Questions
Question 1.
(a) Explain each of the following concepts, along with at least one suitable example for each:
(i) Fixed-point number representation (ii) round-off error (iii) representation of zero as floating point number (iv) significant digits in a decimal number representation (v) normalized representation of a floating point number (vi) overflow
(b) Explain with suitable example that in computer arithmatics ( i.e., numbers represented in computer, with +, −, *, / as implemented in a computer) the multiplication operation( *) may
some computer numbers a, b and c
(c) Find out to how many decimal places the value 22/ 7 is accurate as an approximation of 3.14159265, where the latter is value of ╥, calculated up to 8 places after decimal ?
(d) Calculate a bound for the truncation error in approximating f(x) = sin x by sin (x) = x − x 3 / (fact 3) + x5 / (fact 5), where −1 =< x =< 1 and (fact n) denotes factorial of n
(e) Obtain Approximate the value of (3.7)—1, using first three terms of Taylor’s series expansion.
Question 2.
(a) Solve the system of equations
4 x1+ x2+ 2X3 = 16
2×1 + 5×2 + 3×3 = 19
3×1+ 2×2 − x3 = 12
using Gauss elimination method with partial pivoting.
(b) Perform four iterations (rounded to four decimal places) using
(i) Jacobi Method and
(ii) Gauss-Seidel method ,
for the following system of equations.
Which method gives better approximation to the exact solution?
Question 3.
(a) Determine the smallest roots of the following equation:
f(x) = x2cos (x) + sin (x) =0 to three significant digits using
(i) Regula-falsi method (ii) Newton Raphson method (iii) Bisection method (iv) Secant method
Question 4.
(a) Explain what is the role of interpolation in solving numerical problems?
(b) Express Δ3 f1 as a backward difference.
(c) Express Δ3 f1 as a central difference.
(d) For the following data develop difference table and find forward differences and backward differences
Question 5.
(a) By decinnial census, the population of a town was given below.
Year (x) : 1971 1981 1991 2001 2011
Population (y): 112 132 158 189 226 (in thousands)
(i) Using Stirling’s central difference formula, estimate the population for the year 2006
(ii) Using Newton’s forward formula, estimate the population for the year 1992.
(iii) Using Newton’s backward formula, estimate the population for the year 1980.
b) If values of the function f: x y are given as f(1) = −32, f(4) = 08, f(5) = 52, f(7) = 167 find the Lagrange’s interpolation polynomial of f(x). Also, find f(3).
Question 6.
(a) Find the values of the first and second derivatives of f(x) at x = 76 from the following table. Use 0(h2) forward difference method. Also, find Truncation Error (TE) and actual errors.
Question 7.
(a) Compute the value of the integral
Rectangular Rule (ii) Trapezoidal Rule and then (iii) Simpson’s 1/3 Rule
IGNOU BCS-54 (July 2023 – January 2024) Assignment Questions
Q1. (a) Find floating point representation, if possible normalized, in the 4-digit mantissa, two digit exponent, if necessary use approximation for each of the following numbers:
(i) 27.94 (ii) -0.00943 (iii) -6781014 (iv) 0.0644321
Also, find absolute error, if any, in each
(b) Convert the decimal integer -465 to binary using both the methods (as shown in Pg No:16 of Block-1). Show all the steps.
(c) Convert the number given as binary fraction –(0.101110101)2 to decimal.
(d) Find the sum of the two floating numbers x1=0.1364X101 and x2=0.7342X10-1. Further express the result in normal form, using (i) Chopping (ii) Rounding. Also, find the absolute error.
Q2. (a) Solve the system of equations
2 x + y + z = 3
x + 3y + 3z = 4
x – 4y + 2z = 9
using Gauss elimination method with partial pivoting. Show all the steps.
(b) Perform four iterations (rounded to four decimal places) using
(i) Jacobi Method and
(ii) Gauss-Seidel method ,
for the following system of equations
Which method gives better approximation to the exact solution?
Q3. Determine the smallest positive root of the following equation:
f(x) ≡ x3 – 9×2 – x + 9 = 0
to three significant digits using
(a) Regula-falsi method (b) Newton-Raphson method
(c) Bisectionmethod (d) Secant method
Q4. (a) Find Lagrange’s interpolating polynomial for the following data. Hence obtain the value of f(4).
(b) Using the inverse Lagrange’s interpolation, find the value of x when y=3 for the following data:
Q5. (a) The population of a country for the last 25 years is given in the following table:
(i) Using Stirling’s central difference formula, estimate the populationfor the year 2007
(ii) Using Newton’s forward formula, estimate the population for theyear 1998.
(iii) Using Newton’s backward formula, estimate the population for theyear 2013.
(b) Derive the relationship for the operators δ in terms of E.
Q6. (a) Find the values of the first and second derivatives of y = f(x) for x=2.1 using the following table. Use forward difference method. Also, find Truncation Error (TE) and actual errors.
(b) Find the values of the first and second derivatives of y = f(x) for x=2.1 from the following table using Lagrange’s interpolation formula. Compare the results with (a) part above.
Q7. Compute the value of the integral
By taking 8 equal subintervals using (a) Trapezoidal Rule and then (b) Simpson’s 1/3 Rule. Compare the result with the actual value.