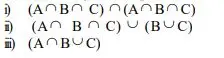PLEASE MATCH YOUR ASSIGNMENT QUESTIONS ACCORDING TO YOUR SESSION
IGNOU MCS-13 (July 2024 – January 2025) Assignment Questions
IGNOU MCS-13 (July 2023 – January 2024) Assignment Questions
Q1. (a) What is Set? Explain use of Set with examples
(b) Make truth table for followings.
(c) Give geometric representation for followings:
i) {5, -3) x ( -2, -2)
ii) {-1, 3) x ( -2, 3)
Q2. (a) Draw Venn diagram to represent followings:
(b) Write down suitable mathematical statement that can be represented by the following symbolic properties.
(c) Show whether √7 is rational or irrational.
Q3. (a) Explain use of inclusion-exclusion principle with example.
(b) Make logic circuit for the following Boolean expressions:
i) (xyz) + (xyz)’ + (xz’y)
ii) ( x’yz) (xyz’) (xy’z)
(b) What is a tautology? If P and Q are statements, show whether the statement
(𝑃 → 𝑄) ∨ ( →~ 𝑃) is a tautology or not.
Q4. (a) How many words can be formed using letter of “EXCELLENT” using each letter at most once?
i) If each letter must be used,
ii) If some or all the letters may be omitted.
(b) What is a relation? What are different types of relation? Explain equivalence relation with the help of example.
(d) What is counterexample? Explain its use with the help of an example.
Q5. (a) How many different professionals committees of 8 people can be formed, each containing at least 2 Doctors, at least 2 Public Servants and 1 IT Expert from list of 7 Doctors, 6 Public Servants and 6 IT Experts?
(b) A and B are mutually exclusive events such that P(A) = 1/2 and P(B) = 1/3 and P (AU B) = 1/4. What is the probability of P(A Ո B)?
(c) Find how many 3 digit numbers are odd?
(d) Explain whether the function f(x) = x + 1 is one-one or not.
Q6. (a) How many ways are there to distribute 21 district items into 6 distinct boxes with:
i) At least two empty box.
ii) No empty box.
(b) Explain principle of multiplication with an example.
(c) Three Sets A, B and C are: A = {1, 2,3,4,5, 8,9,12,15,17}, B = { 1,2, 3 ,4,8,9, 10 } and C {1,2,7, 9, 10, 11, 13}.
Q7. (a) Explain addition theorem in probability.
(b) Make Pascal’s triangle up to n = 6.
(c) What is a function? Explain different types of functions with example.
(d) Write the following statements in symbolic form:
(i) Mr. X is poor but happy.
(ii) Either eat healthy food or be ready for poor health.
Q8. (a) Find inverse of the following functions