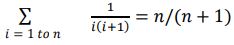Are you looking to download a PDF soft copy of the Solved Assignment MCS-212 - Discrete Mathematics? Then GullyBaba is the right place for you. We have the Assignment available in English language.
This particular Assignment references the syllabus chosen for the subject of Mathematics, for the January 2024 - July 2024 session. The code for the assignment is MCS-212 and it is often used by students who are enrolled in the MCA (Revised) Degree.
Once students have paid for the Assignment, they can Instantly Download to their PC, Laptop or Mobile Devices in soft copy as a PDF format. After studying the contents of this Assignment, students will have a better grasp of the subject and will be able to prepare for their upcoming tests.
PLEASE MATCH YOUR ASSIGNMENT QUESTIONS ACCORDING TO YOUR SESSION
IGNOU MCS-212 (January 2025 – July 2025) Assignment Questions
Q1: Prove by mathematical induction that
Q2: Verify whether √11 is rational or irrational.
Q3: Write the following statements in the symbolic form.
i) Some students can not appear in exam.
ii) Everyone can not sing.
Q4: Draw logic circuit for the following Boolean Expression:
(x y z) + (x+y+z)’+ (x’zy’)
Q5: Explain whether function: f(x) = x2 posses an inverse function or not.
Q6: Write the finite automata corresponding to the regular expression (a + b)*ab
Q7: If L1 and L2 are context free languages then, prove that L1 U L2 is a context free language.
Q8: Explain Decidable and Undecidable Problems. Give example for each.
Q9: What is equivalence relation? Explain use of equivalence relation with the help of an example
Q10: There are three Companies, C1, C2 and C3. The party C1 has 4 members, C2 has 5 members and C3 has 6 members in an assembly. Suppose we want to select two persons, both from the same Company, to become president and vice president. In how many ways can this be done?
Q11: How many words can be formed using letter of DEPARTMENT using each letter at most once?
i) If each letter must be used,
ii) If some or all the letters may be omitted.
Q12: What is the probability that a number between 1 and 10,000 is divisible by neither 2, 3, 5 nor 7?
Q13: Explain inclusion-exclusion principle and Pigeon Hole Principle with example.
Q14: Find an explicit recurrence relation for minimum number of moves in which the n-disks in tower of Hanoi puzzle can be solved! Also solve the obtained recurrence relation through an iterative method.
Q15: Find the solution of the recurrences relation an = an-1 + 2an-1, n > 2 with a0 = 0, a1=1
Q16: Prove that the complement of
Q17: What is a chromatic number of a graph? What is a chromatic number of the following graph?
Q18: Determine whether the above graph has a Hamiltonian circuit. If it has, find such a circuit. If it does not have, justify it.
Q19: Explain and prove the Handshaking Theorem, with suitable example.
Q20: Explain the terms PATH, CIRCUIT and CYCLES in context of Graphs.
IGNOU MCS-212 (January 2024 – July 2024) Assignment Questions
Q1: Use Mathematical Induction to prove that: 12 + 22 + ……..+ n2 = n(n+1)(2n+1)/6
Q2: How many different permutations arepossible of the letters, taken all at a time, of the word:
ASSESSES?
Q3: A die is rolled once. What are the probabilities of the following events:
a. Getting an odd number
b. Getting at least a value 2
c. Getting at most a value 2
d. Getting at least 7
Q4: Draw a hypercube graph Q3 (also called the cubical hypercube). Check whether the hypercube Q3 is Hamiltonian
Q5: What is isomorphism? Find, if the following graphs G1 and G2 are isomorphic or not. Explain how you arrived at your answer.
Q6: What is a finite automata? Why is it needed? How is a finite automata represented? Also explain the term regular expression with the help of an example.
Q7: Differentiate between
a. Deterministic and Non-deterministic finite automata
b. Deterministic and Non-deterministic Turing Machine
c. Moore and Mealy Machine
Q8: Describe the divide-and-conquer approach to solve recurrences? Explain how this approach can be used to apply binary search in a sorted list.
Q9: What is proposition? Explain with the help of an example. Explain Disjunction and Conjunction with the help of truth table for each.
Q10: Prove the following theorem by direct proof method: ‘‘The square of an even integer is an even integer.’’
Q11: Given the Boolean expression (a′ ∨ (b ∧ c′)) ∨ (b ∨ d′),draw the corresponding circuit, where a, b, c and d are the inputs to the circuitry.
Q12: Define the terms Domain, Co-domain and Range in the context of a function. Also find the domain, co-domain and range for a function A to B, where A = {1,2,3,4} and B = {1,4,9,16,25}.
Q13: A committee consisting of 2 male and2 female workers is to be constituted from 8 male and 9 female workers. In how many distinct ways can this be done?
Q14: In a tennis tournament, each entrant plays a match in the first round. Next, all winners from the first round play a second-round match. Winners continue to move on to the next round, until finally only one player is left as the tournament winner. Assuming that tournaments always involve n = 2k players, for some k, find the recurrence relation for the number rounds in a tournaments of n players.
15: Show, using the pigeonhole principle, that in any group of 30 people, 5 people can always be found who were born on the same day of the week.
Q16: Define the following in the context of graph, with the help of an example:
a. Complete graph
b. Degree of a vertex
c. Cycle
d. Path
e. Circuit
Q17: What is a bipartite graph ? Explain with the help of an example. Give one or two applications of bipartite graphs.
Q18: How Hamiltonian graphs differ from the Eulerian graphs? Give Dirac’s and Ore’s criterion for the Hamiltonian graphs.
Q19: Differentiate between Eulerian graph and Eulerian circuit. Find the Eulerian circuit in the graph given below(if it exists).
Q20: Write Short notes on following
a. Travelling Salesman Problem
b. Vertex Coloring
c. Edge Coloring
d. Planar graphs
e. Pascal’s Formula
The IGNOU open learning format requires students to submit study Assignments. Here is the final end date of the submission of this particular assignment according to the university calendar.
30th April (if Enrolled in the June Exams)
31st October (if Enrolled in the December Exams).
What’s Included
In this section you can find other relevant information related to the Assignment you are looking at. It will give you an idea of what to expect when downloading a PDF soft copy from GullyBaba.
All Solved Answers By IGNOU Experts.
Available for 3 Times for Download.
Downloadable Soft Copy in PDF.
Print Ready Format: A4 (21 x 29 x .20 cm (Width x Length x Height)
Help?
