PLEASE MATCH YOUR ASSIGNMENT QUESTIONS ACCORDING TO YOUR SESSION
IGNOU MCH-13 (January 2025 – December 2025) Assignment Questions
1. Answer any five of the following in brief.
a) Give the physical significance of Helmholtz energy.
b) What is the effect of temperature on chemical potential?
c) Explain the molecular partition function in brief.
d) What is the improper rotation of the molecules? Explain with a suitable example.
e) Give the characteristics of the unimolecular reactions.
f) Define the primary and secondary salt effects on the rate of reactions in solution.
g) Why the conventional kinetic methods are not useful to study the fast reactions?
2. (a) Determine the conditions for the spontaneity and equilibrium for following combinations of ΔH and ΔS for a given process
(b) (i) Two moles of an ideal gas expand isothermally at 300 K from 7 bar to 3 bar. Calculate the change in the Helmholtz energy and Gibbs energy for the process.
(ii) Define partial molar volume and give its physical significance.
3. (a) Give Stirling’s approximation and outline its significance. Calculate the % error introduced in computing the value of 10! by using this approximation. (Given ln 2= 0.69 and ln 3= 1.01)
(b) (i) A system consist of two energy level 0 and 1 which are singly and triple degenerate, respectively. Calculate the partition function of the system.
Or
Derive the relation between molecular and canonical partition function.
(ii) Derive an expression for the rotational partition function.
4. (a) (i) Define Tetrahedral and Octahedral voids in three dimensional close packing.
ii) If atoms of element B form HCP lattice and 2/3rd of tetrahedral voids are occupied by those of the element A,what is the formula of the compound formed by the elements A and B?
(iii) State the law of constancy of interfacial angles.
(b) (i) Show the following planes in cubic unit cells
i) (110) in Primitive cubic cell
ii) (111) in Face-centred cubic cell and
iii) (200) in Body-centred cubic cell.
(ii) Give the difference between screw Axis and glide Plane by using suitable illustrations.
or
Identify all the symmetry elements in trans C2H2Cl2 or B2Cl6
5. (a) Give the salient features ofthe collision theory and calculate the factor that relates the collision theory with Arrhenius Equation.
(b) (i) Discuss the Lindemann-Christiansen mechanism for unimolecular reactions and give the Hinshelwood’s modification of this mechanism.
(ii) What are two important features of the expression for rate of activation as per RRK theory?
6. Answer any five of the following in brief.
a) Give the principle of ultrasonic relaxation methods for the determination of the rates of the fast reactions.
b) Explain the difference between homogeneous and heterogeneous catalysis with suitable examples.
c) Describethe lock and key hypothesis of the enzyme action.
d) What is the role of solvent in the Debye-Huckel model of a solution of an electrolyte?
e) Why did we need the modification in the Debye-Huckel theory?
f) Give the mathematical expressions of any two type of Maxwell and Boltzmann distribution of molecular speeds and name the terms involved.
g) What is the effect of pressure and temperature on thermal conductivity?
7. (a) Derive the expression of the rate constant for reactions in solution in terms of activity where the reference standard state for the reactants is the gaseous state.
(b) (i) What is the difference between diffusion controlled and activation-controlled reactions.
(ii) Discuss the stopped flow method for the study of fast-reactions with suitable schematic diagram and outline its advantages over continuous flow method.
8. (a) What is adsorption in homogeneous catalysis? Derive an expression for Langmuir monolayer adsorption isotherms for adsorption at sufficiently low concentrations.
(b) (i) What is the difference between competitive and uncompetitive enzyme inhibition?
(ii) Derive the mathematical rate expression for competitive enzyme inhibition and give the graphical representation of Lineweaver-Burk plot.
9. (a) (i) Write the basic assumptions of the Debye-Huckel theory.
(ii) Calculate the ionic strength of
i) 0.08 mol kg-1 solutions of Ca(NO3)2 and
ii) the solution consisting of 6.3 g of MgCl2, 5 g of AlCl3 and 500 g of water.
(b) (i) List different methods of experimental determination of activity coefficients.
(ii) Explain the principle for the experimental determination of activity and activity coefficient from solubility measurements.
10. (a) (i) What are the limitations of phenomenological approach to transport properties?
(ii) Using the Fick’s first law of diffusion, derive the mathematical expression that provides the link between the phenomenological and thermodynamic treatment of diffusion phenomenon.
(b) (i) Why is conductivity not a suitable quantity to compare the conduction behaviour of different electrolytic solutions?
(ii) Define thermal conductivity. Why the thermal conductivity of gases is independent of pressure up to a reasonably high pressure.
IGNOU MCH-13 (January 2024 – December 2024) Assignment Questions
1. Answer any five of the following in brief.
(a) The entropy change is not a good criterion for spontaneity of a thermodynamic process. Comment.
(b) Derive the relation between Gibbs energy and Helmholtz energy.
(c) Differentiate between molar and partial molar properties.
(d) Give Stirling’s approximation and outline its significance
(e) How can the diamagnetic and paramagnetic substances be distinguished using magnetic susceptibilities?
(f) Outline the limitations of collision theory.
2. (a) (i) An isothermal and isobaric process is accompanied by changes in enthalpy and entropy as 52 kJ mol-1 and 165 JK-1 mol-1 , respectively. Predict whether the process be spontaneous at 400K.
(ii) If the enthalpy and entropy changes are not affected by the change in temperature calculate the temperature at which the system will attain equilibrium
(b) Define the term ‘chemical potential’ and discuss the effect of temperature on chemical potential.
3. (a) Explain the difference between permutation and configuration. Calculate the number of permutations and configurations possible while selecting three days out of seven days in a week.
(b) Define molecular partition functions. Derive an expression for the translational partition function for motion along x- direction in a system.
4. (a) The X-ray power diffraction angles from the molybdenum crystal are observed at 20.26°, 29.30°, 36.82°, 43.82°, 50.70°, 58.80°, 66.30°. Determine the type of cubic crystal formed by molybdenum?
(b) Explain crystal symmetry elements, Screw Axis and Glide Plane using suitable illustrations.
5. (a) Describe the basic premise of transition state theory of reaction rates and derive an expression by using this theory for the rate constant for the elementary reaction X + Y ® Products
(b) Discuss Lindemann-Christiansen mechanism for unimolecular reactions and derive an expression for the rate equation for the unimolecular reaction as per Lindemann Christiansen mechanism.
6. Answer any five of the following in brief.
(a) Discuss the role of solvent in reactions in solution phase.
(b) Define fast reactions and give different strategies used for studying fast reactions.
(c) Define enzyme inhibition and state it’s different types.
(d) Define ionic strength and calculate the same for an aqueous solution of 0.1 M MgCl2.
(e) Differentiate between true and potential electrolytes.
(f) Differentiate between the phenomenon of Osmosis and Dialysis.
(g) State Fick’s second law of diffusion and give its significance.
7. (a) Describe the encounter pair description of reaction in solution and derive the expression for the rate of a reaction in solution in terms of this description.
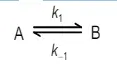
(b) In a Temperature-jump experiment the relaxation time of an equilibrium reaction of the type
is found to be 5 µs. in a separate experiment, the equilibrium constant for the reaction is found to be 5 x 10-4, calculate the values of rate constants for the forward and backward reactions.
8. (a) Define homogeneous catalytic reactions and derive the expression for the initial reaction rate of a homogeneous catalytic reaction.
(b) Give the Michaelis–Menten mechanism of enzyme catalysed reactions and derive an expression for the rate of enzymatic reaction using this mechanism.
9. (a) Define mean ionic mobility and formulate the relations between mean ionic molality (m±) and m for the following electrolytes:
Li2SO4, MgCl2 and Na3PO4
(b) Explain the principle for the experimental determination of mean ionic activity by emf measurement.
10. (a) Define coefficient of viscosity and derive the relationship between the coefficient of viscosity and mean free path.
(b) Define ionic mobility and derive the relationship between the ionic mobility and molar conductivity.