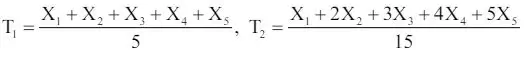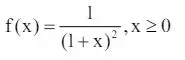PLEASE MATCH YOUR ASSIGNMENT QUESTIONS ACCORDING TO YOUR SESSION
IGNOU MST-16 (June 2024 – June 2025) Assignment Questions
1. (a) State whether the following statements are True or False. Give reason in support of your answer:
(i) If X1, X2, X3, X4 and X5 is a random sample of size 5 taken from an Exponential distribution, then estimator T1 is more efficient than T2.
(ii) If T1 and T2 are two estimators of the parameter θ such that Var(T1) = 1/n and Var(T2) = n then T1 is more efficient than T2.
(iii) A 95% confidence interval is smaller than 99% confidence interval.
(iv) If the probability density function of a random variable X follows F-distribution is
then degrees of freedom of the distribution will be (2,2).
(v) A patient suffering from fever reaches to a doctor and suppose the doctor formulate the hypotheses as
H0: The patient is a chikunguniya patient
H1: The patient is not a chikunguniya patient
If the doctor rejects H0 when the patient is actually a chikunguniya patient, then the doctor commits type II error.
(b) Describe the various forms of the sampling distribution of ratio of two sample variances.
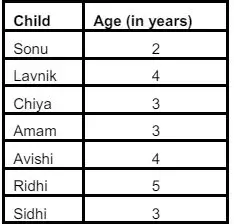
2. A baby-sister has 6 children under her supervision. The age of each child is as follows:
(i) What is the form of population of age of children?
(ii) Prepare the sampling distribution of sample mean when sample size is 2.
(iii) Is the shape of the sampling distribution normal?
(iv) Calculate the mean and standard error of the sampling distribution.
3. The department of transportation has mandated that the average speed of cars on interstate highways be no more than 70 km per hours in order. To check that the people follow it or not,a researcher took a random sample of 186 cars and found that the average speed was 72 km per hours with a standard deviation 0.6 km per hours.
(a) Construct the interval around the sample mean that would contain the population mean 95% of the time.
(b) If the researcher wants to test that the true mean speed on its highways is 70 km per hours or less with 95% confidence then
(i) State null and alternative hypotheses.
(ii) Name the test which is suitable in this situation and why?
(iii) Calculate the value of test statistic and critical value.
(iv)Draw the conclusion on the basis of the applied test.
4(a) A sample of 500 shops was selected in a large metropolitan area to determine various information concerning consumer behaviour. One question, among the questions, asked, was “Do you enjoy shopping for clothing?” Out of 240 males 136 answered yes. Out of 260 females, 224 answered yes. Find 95% confidence interval for the difference of the proportions for enjoys shopping for clothing.
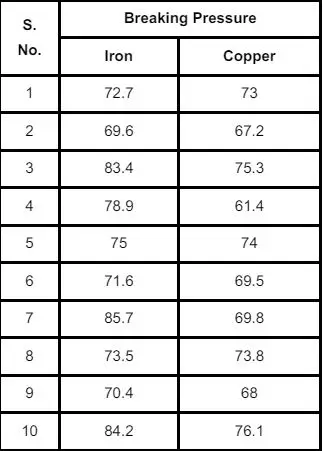
(b) An engineer conducted an experiment to compare two metals: iron and copper, as bonding agents for an alloy material. Components of the alloy were bonded using the metals as bonding agents, and the pressures required to break the bonds were measured. The data for the breaking pressures are given in the following table:
If the breaking pressures for both iron and copper are normally distributed, are the variances of the distributions of the breaking pressure of iron and copper equal at 5 % level of significance?
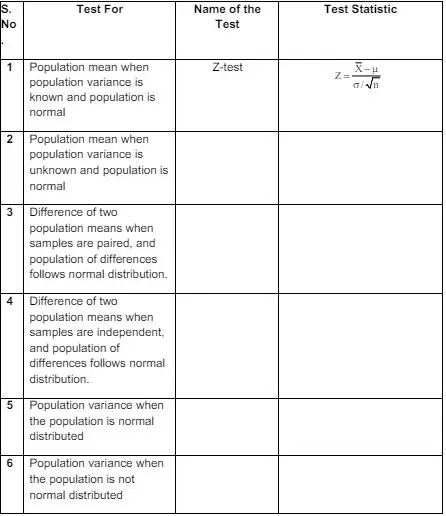
5. (a) Complete the following table, one is done for you:
(b) Describe the following:
(i) Curve of F-distribution
(ii) Mean Squared Error
IGNOU MST-16 (January 2024 – December 2024) Assignment Questions
1. (a) State whether the following statements are True or False. Give reason in support of your answer:
(i) If X1, X2, X3, X4 and X5 is a random sample of size 5 taken from an Exponential distribution, then estimator T1 is more efficient than T2.
(ii) If T1 and T2 are two estimators of the parameter θ such that Var(T1) = 1/n and Var(T2) = n then T1 is more efficient than T2.
(iii) A 95% confidence interval is smaller than 99% confidence interval.
(iv) If the probability density function of a random variable X follows F-distribution is
then degrees of freedom of the distribution will be (2,2).
(v) A patient suffering from fever reaches to a doctor and suppose the doctor formulate the hypotheses as
H0: The patient is a chikunguniya patient
H1: The patient is not a chikunguniya patient
If the doctor rejects H0 when the patient is actually a chikunguniya patient, then the doctor commits type II error.
(b) Describe the various forms of the sampling distribution of ratio of two sample variances.
2. A baby-sister has 6 children under her supervision. The age of each child is as follows:
(i) What is the form of population of age of children?
(ii) Prepare the sampling distribution of sample mean when sample size is 2.
(iii) Is the shape of the sampling distribution normal?
(iv) Calculate the mean and standard error of the sampling distribution.
3. The department of transportation has mandated that the average speed of cars on interstate highways be no more than 70 km per hours in order. To check that the people follow it or not,a researcher took a random sample of 186 cars and found that the average speed was 72 km per hours with a standard deviation 0.6 km per hours.
(a) Construct the interval around the sample mean that would contain the population mean 95% of the time.
(b) If the researcher wants to test that the true mean speed on its highways is 70 km per hours or less with 95% confidence then
(i) State null and alternative hypotheses.
(ii) Name the test which is suitable in this situation and why?
(iii) Calculate the value of test statistic and critical value.
(iv)Draw the conclusion on the basis of the applied test.
4(a) A sample of 500 shops was selected in a large metropolitan area to determine various information concerning consumer behaviour. One question, among the questions, asked, was “Do you enjoy shopping for clothing?” Out of 240 males 136 answered yes. Out of 260 females, 224 answered yes. Find 95% confidence interval for the difference of the proportions for enjoys shopping for clothing.
(b) An engineer conducted an experiment to compare two metals: iron and copper, as bonding agents for an alloy material. Components of the alloy were bonded using the metals as bonding agents, and the pressures required to break the bonds were measured. The data for the breaking pressures are given in the following table:
If the breaking pressures for both iron and copper are normally distributed, are the variances of the distributions of the breaking pressure of iron and copper equal at 5 % level of significance?
5. (a) Complete the following table, one is done for you:
(b) Describe the following:
(i) Curve of F-distribution
(ii) Mean Squared Error